Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 36
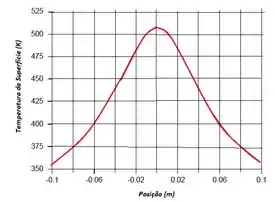
Um longo elemento aquecedor cilíndrico com 20 mm de diâmetro, operando a 700 K em meio ao vácuo, está posicionado a 40 mm de uma parede isolada de baixa condutividade térmica.
- Admitindo que o elemento e a parede sejam negros, estime a temperatura máxima atingida pela parede quando a vizinhança está a 300 K.
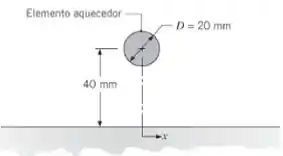
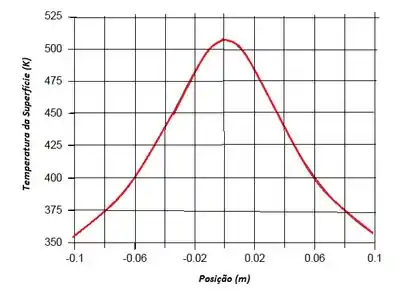
- Calcule e represente graficamente a distribuição de temperaturas na parede em regime estacionário no intervalo –100 mm ≤ x ≤ 100 mm.
Passo 1
Vamos que vamos galerinha ?!
Bom, na letra (a) nós queremos achar estime a temperatura máxima atingida pela parede, quando a vizinhança está a 300 K, não é?
Para isso nós precisamos de fazer o balanço de energia para a parede, que estão recebendo calor por condução e perdendo por radiação para o elemento aquecedor e para a superfície:
Como a parede está isolada e possui baixa condutividade térmica, a transferência de calor por condução pode ser negligenciada:
Pelo somatório dos fatores de forma para a parede:
Substituindo:
Vamos ver o que temos?
Bom, nós ainda não temos os fatores de forma, não é?
Passo 2
Os fatores de forma são tabelados, não é? No caso de cilindro e retângulo paralelos:
Onde:
Então:
Por expansão em série de Taylor, quando nós podemos fazer uma aproximação:
Então:
A temperatura máxima vai ocorrer quando e lembrando que:
Então:
Agora é só achar a temperatura:
Finalizamos a letra (a), mas ainda não terminamos !!
Passo 3
A letra (b) nos pede para representar graficamente a distribuição de temperaturas na parede em regime estacionário no intervalo
Então nós faremos o Passo 1 e 2 novamente, somente variando posição x, e para isso vamos utilizar um software:
Sucessooo galerinhaa, terminamos mais umaa !!
