Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 41

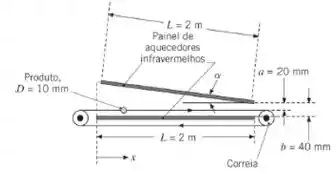
Muitos produtos são processados de uma maneira que requer uma temperatura do produto especificada como uma função do tempo. Considere um produto com a forma de um longo cilindro, com 10 mm de diâmetro, que é transportado lentamente através de um forno de

processamento como mostrado na figura. O produto exibe um comportamento próximo ao de um corpo negro e é fixado à correia de transporte pelas suas extremidades. A vizinhança está a 300 K, enquanto os aquecedores na forma de painéis radiantes estão a 500 K e têm superfícies que exibem um comportamento próximo ao de um corpo negro. Um engenheiro propõe um novo projeto de forno com uma superfície superior inclinada de modo a ser capaz de mudar rapidamente a resposta térmica do produto.

  1. Determine a radiação por unidade de comprimento incidente sobre o produto em x = 0,5 m e x = 1 m, para α = 0.
  2. Determine a radiação por unidade de comprimento incidente sobre o produto em x = 0,5 m e x = 1 m, para α = π/15.

Sugestão: O fator de forma do cilindro para a vizinhança no lado esquerdo pode ser encontrado pela soma dos fatores de forma do cilindro para as duas superfícies mostradas com tracejado vermelho na figura.

Passo 1

É isso aí galerinha !! Vamos continuar?!

Primeiro vamos especificar no desenho as superfícies que estarão presentes, certo?

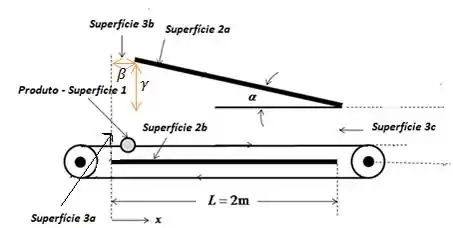
A letra (a) nos pediu para achar a radiação incidente sobre o produto, ou seja, a superfície 1! Como temos as superfícies 2 e 3 presentes aqui:

q e n t r a = q 21 + q 31

Substituindo o calor:

q e n t r a = A 2 F 21 σ T 1 4 + A 3 F 31 σ T 3 4

Lembrando a reciprocidade:

A 3 F 31 = A 1 F 13 = π D L . F 13

A 2 F 21 = A 1 F 12 = π D L . F 12

E usando o somatório para a superfície 1:

F 12 + F 13 = 1   →     F 12 = 1 - F 13  

Substituindo:

q e n t r a = π D L 1 - F 13 σ T 1 4 + π D L F 13 σ T 3 4

Como nós queremos o calor por unidade de comprimento:

q e n t r a L = π D σ 1 - F 13 T 1 4 + F 13 T 3 4

Agora nós vamos ver o que temos aqui:

D = 0,01   m

σ = 5,67 × 10 - 8 W m 2 K 4

T 1 = 500   K

T 3 = 300   K

Então a única coisa que precisamos é achar o fator de forma F 13 !!

Bom, pelo desenho nós vimos que existe a superfície 3a, 3b e 3c, então:

F 13 = F 13 a + F 13 b + F 13 c

Passo 2

Bom, olhamos na Tabela 13.1 nós podemos calcular o fator de forma para o caso de cilindros e retângulos paralelos:

F i j = r s 1 - s 2 tan - 1 ⁡ s 1 L - tan - 1 ⁡ s 2 L

Como o nosso interesse aqui é achar F j i , vamos usar a reciprocidade:

F j i = A i F i j A j = s 1 - s 2 F i j 2 π r

Então:

F j i = s 1 - s 2 2 π r . r s 1 - s 2 tan - 1 ⁡ s 1 L - tan - 1 ⁡ s 2 L

F j i = 1 2 π tan - 1 ⁡ s 1 L - tan - 1 ⁡ s 2 L

Para a superfície 3a, quando α = 0 :

s 1 = a

s 2 = - ( b - a )

L = x

Substituindo:

F 13 a = 1 2 π tan - 1 ⁡ a x - tan - 1 ⁡ - ( b - a ) x

Para x = 0,5 m :

F 13 a = 1 2 π tan - 1 ⁡ 0,02 0,5 - tan - 1 ⁡ - ( 0,04 - 0,02 ) 0,5 = 0,0127

Para x = 1,0 m :

F 13 a = 1 2 π tan - 1 ⁡ 0,02 1 - tan - 1 ⁡ - ( 0,04 - 0,02 ) 1 = 0,0064

Quando α = 0 nós temos que A 3 b = 0 e, portanto, F 13 b = 0 !!

Para a superfície 3c, quando α = 0 :

s 1 = a

s 2 = - ( b - a )

L = L - x

Substituindo:

F 13 c = 1 2 π tan - 1 ⁡ a L - x - tan - 1 ⁡ - ( b - a ) L - x

Para x = 0,5 m :

F 13 c = 1 2 π tan - 1 ⁡ 0,02 2 - 0,5 - tan - 1 ⁡ - ( 0,04 - 0,02 ) 2 - 0,5 = 0,0 042

Para x = 1,0 m :

F 13 c = 1 2 π tan - 1 ⁡ 0,02 2 - 1 - tan - 1 ⁡ - ( 0,04 - 0,02 ) 2 - 1 = 0,0064

Agora é só fazer o somatório!!

Quando x = 0 , 5   m :

F 13 = 0,0127 + 0 + 0,0042 = 0,0169

Quando x = 1 , 0   m :

F 13 = 0,0064 + 0 + 0,0064 = 0,0128

Sucesso !!!

Agora vamos por no calor??

Quando x = 0 , 5   m :

q e n t r a L = π 0,01 5,67 × 10 - 8 1 - 0,0169 500 4 + 0,0169 300 4

q e n t r a L = 109,6 W m

Quando x = 1 , 0   m :

q e n t r a L = π 0,01 5,67 × 10 - 8 1 - 0,0128 500 4 + 0,0128 300 4

q e n t r a L = 110 W m

E assim nós finalizamos a letra (a) !!

Passo 3

Na letra (b) nós teremos que fazer o passo 2 novamente, mas agora teremos que considerar α = π 15 !!

Para a superfície 3a:

F 13 a = 1 2 π tan - 1 ⁡ s 1 + γ x - tan - 1 ⁡ s 2 x

Com auxílio da trigonometria:

γ = L . sin ⁡ α = 2 sin ⁡ π 15

Para x = 0,5 m :

F 13 a = 1 2 π tan - 1 ⁡ 0,02 + 2 sin ⁡ π 15 0,5 - tan - 1 ⁡ - ( 0,04 - 0,02 ) 0,5 = 0,12 05

Para x = 1,0 m :

F 13 a = 1 2 π tan - 1 ⁡ 0,02 + 2 sin ⁡ π 15 1 - tan - 1 ⁡ - ( 0,04 - 0,02 ) 1 = 0,06 86

Para a superfície 3b:

F 13 b = 1 2 π tan - 1 ⁡ x a + γ - tan - 1 ⁡ x - β a + γ

Com auxílio da trigonometria:

β = L . ( 1 - co s ⁡ α ) = 2 1 - cos ⁡ π 15

Para x = 0,5 m :

F 13 b = 1 2 π tan - 1 ⁡ 0,5 0,02 + 2 sin ⁡ π 15 - tan - 1 ⁡ 0,5 - 2 1 - cos ⁡ π 15 0,02 + 2 sin ⁡ π 15 = 0 , 0072

Para x = 1,0 m :

F 13 b = 1 2 π tan - 1 ⁡ 1 0,02 + 2 sin ⁡ π 15 - tan - 1 ⁡ 1 - 2 1 - cos ⁡ π 15 0,02 + 2 sin ⁡ π 15 = 0,0 02 6

Para a superfície 3c:

F 13 c = 1 2 π tan - 1 ⁡ a L - x - tan - 1 ⁡ - b - a L - x

Para x = 0,5 m :

F 13 c = 1 2 π tan - 1 ⁡ 0,02 2 - 0,5 - tan - 1 ⁡ - 0,04 - 0,02 2 - 0,5 = 0,00 4 2

Para x = 1,0 m :

F 13 b = 1 2 π tan - 1 ⁡ 0,02 2 - 1 - tan - 1 ⁡ - 0,04 - 0,02 2 - 1 = 0,00 64

Agora é só fazer o somatório!!

Quando x = 0 , 5   m :

F 13 = 0,12 05 + 0,00 7 2 + 0,0042 = 0 , 1319

Quando x = 1 , 0   m :

F 13 = 0,0 6 86 4 + 0,0026 + 0,0064 = 0,0 776

Sucesso !!!

Agora vamos por no calor??

Quando x = 0 , 5   m :

q e n t r a L = π 0,01 5,67 × 10 - 8 1 - 0,1319 500 4 + 0,1319 300 4

q e n t r a L = 9 8 , 6 W m

Quando x = 1 , 0   m :

q e n t r a L = π 0,01 5,67 × 10 - 8 1 - 0,1319 500 4 + 0,1319 300 4

q e n t r a L = 10 3,9 W m

E chegamos ao fim de mais umaa !!

Resposta

  1. x = 0,5   m : q e n t r a L = 109,6 W m     |     x = 1,0   m : q e n t r a L = 110 W m
  2. x = 0,5   m : q e n t r a L = 9 8 , 6 W m     |     x = 1,0   m : q e n t r a L = 10 3,9 W m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere as cavidades formadas por um cone, um cilindro e uma esfera que têm o mesmo tamanho de abertura (d) e dimensão principal (L), como mostrado na figura.(b) Determine a emissividade efetiva de
Um longo tubo horizontal com paredes delgadas e 100 mm de diâmetro é mantido a 120°C pela passagem de vapor de água através do seu interior. Uma barreira de radiação é instalada ao redor do tubo, cria
13.50 Uma chapa de alumínio anodizado, com espessura de t = 5 mm, é usada para descartar calor em um dispositivo de potência para uso no espaço. A borda da chapa é fixada à fonte quente e a chapa é ma
Considere o sótão de uma casa localizada em um local de clima quente. O piso do sótão é caracterizado por uma largura L 1 = 10 m, enquanto o telhado faz um ângulo de θ = 30° a partir da direção horizo
13.50 Uma chapa de alumínio anodizado, com espessura de t = 5 mm, é usada para descartar calor em um dispositivo de potência para uso no espaço. A borda da chapa é fixada à fonte quente e a chapa é ma