Ar frio a entra em um tubo isotérmico de de diâetro a de comprimento em velocidade de e deixa a . Estime a temperatura da superfície do tubo.
Passo 1
Podemos desenhar o diagrama esquemático do fluxo do tubo da seguinte forma:
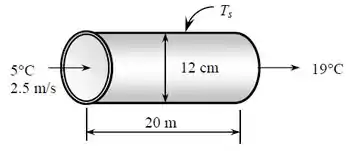
Passo 2
Dados fornecidos:
Temperatura média de entrada do ar:
Temperatura média de saída do ar:
Velocidade média do fluxo de ar:
Diâmetro do tubo:
Comprimento do tubo:
Premissas:
1) Existem condições operacionais estáveis.
2) A superfície interna do duto é lisa.
3) O ar é um gás ideal com propriedades constantes.
4) A pressão do ar é de 1 atm.
Passo 3
Podemos começar calculado a temperatura média do filme para obter as propriedades do ar. Assim temos:
Aqui é a temperatura média do filme, é a temperatura de entrada do ar e é a temperatura de saída do ar.
Com a temperatura de filme, podemos obter as propriedades do ar na Tabela A-15 “Propriedades do ar a de pressão” registradas na temperatura de , interpolando linearmente os valores em e . Assim temos:
Densidade:
Calor específico:
Condutividade térmica:
Viscosidade cinemática:
Número de Prandtl:
Passo 4
Agora, vamos calcular o número de Reynolds usando a seguinte expressão:
Aqui, é o número de Reynolds, é a velocidade média do ar no tubo, é o diâmetro interno do tubo e é a viscosidade cinemática. Substituindo os termos da equação pelos dados obtidos, temos:
Como o número de Reynolds é superior a , o fluxo é turbulento.
Passo 5
Vamos agora calcular os comprimentos de entrada neste caso. Assim temos:
Aqui, é o comprimento da entrada hidrodinâmica e é o comprimento da entrada térmica. Substituindo os termos da equação pelos dados obtidos, temos:
O comprimento da entrada é muito menor que o comprimento especificado do tubo . Portanto, é um fluxo turbulento totalmente desenvolvido em todo o tubo.
Passo 6
Agora, podemos calcular o número de Nusselt pela equação de Dietus-Boelter. Assim temos:
Substituindo os termos da equação pelos dados obtidos, temos:
Com o número de Nusselt, podemos calcular o coeficiente de transferência de calor por convecção dentro do tubo. Assim temos:
Portanto, coeficiente de transferência de calor é
Substituindo os termos da equação pelos dados obtidos, temos:
Passo 7
Calcule a vazão mássica do ar no tubo.
Agora, vamos encontrar uma expressão para a vazão mássica do ar no tubo:
Onde a é área de seção transversal do tubo.
Assim temos:
Passo 8
Agora, vamos calcular a temperatura na superfície do tubo usando a seguinte relação:
Onde é a temperatura de superfície do tubo, é a temperatura média de saída, é a temperatura média de entrada, é o coeficiente de transferência de calor por convecção dentro do tubo, é a vazão mássica, é o calor específico da água e é a área da superfície do tubo .
Substituindo os termos da equação pelos dados obtidos, temos:
Assim, a temperatura da superfície do tubo é .