Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 8.Problemas - Ex. 96
Óleo a deve ser aquecido por vapor saturado a em trocador de calor de tubo duplo até a temperatura de . Os diâmetros internos e externos do espaço anular são e , respectivamente, e o óleo entra a uma velocidade média de . O tubo interno pode ser considerado isotérmico a , e o tubo externo está bem isolado. Considerando que o escoamento de óleo é completamente desenvolvido, determine o comprimento do tubo necessário para aquecer o óleo na temperatura indicada. Será necessário um tubo mais curto ou mais longo? Explique.
Passo 1
Podemos desenhar o diagrama esquemático do fluxo do tubo da seguinte forma:
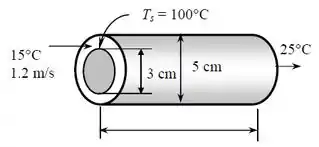
Passo 2
Dados fornecidos:
Velocidade média do fluxo de óleo:
Temperatura média de entrada:
Temperatura média de saída:
Temperatura da superfície interna do tubo:
Diâmetro interno:
Diâmetro externo:
Premissas:
1) Existem condições operacionais estáveis.
2) As superfícies do tubo são lisas.
Passo 3
Para resolver a questão, começamos calculando a temperatura média do óleo com a seguinte relação:
Aqui, é a temperatura média de entrada e é a temperatura média de saída do óleo. Substituindo os termos pelos dados fornecidos no enunciado, temos:
Com o valor da temperatura média, podemos obter as seguintes propriedades óleo em na Tabela A-13 “Propriedades dos líquidos - Óleo do motor (não utilizado)”.
Densidade:
Condutividade térmica:
Viscosidade cinemática:
Calor específico:
Número e Prandtl:
Passo 4
Podemos começar calculando o diâmetro hidráulico usando a seguinte equação:
Aqui, é a área da seção transversal do anel, é o perímetro do anel.
Temos que a área da seção transversal é:
Aqui, e são os diâmetros externo e interno do espaço anular, respectivamente.
Passo 5
Vemos agora calcular o número de Reynolds usando a seguinte equação:
Substituindo os termos pelos dados fornecidos no enunciado, temos:
Como o número de Reynolds é inferior a , o fluxo através do anel é laminar.
Vamos agora calcular o comprimento da entrada hidrodinâmica usando a seguinte equação:
Substituindo os termos pelos dados fornecidos no enunciado, temos:
O comprimento da entrada do limite térmico é determinado com a seguinte relação:
Substituindo os termos pelos dados fornecidos no enunciado, temos:
Passo 6
Agora, vamos calcular a área da seção transversal do anel em que o óleo está fluindo. Como o óleo flui através do espaço anular, temos:
Substituindo os termos pelos dados fornecidos no enunciado, temos:
Agora, vamos calcular a vazão mássica usando a seguinte equação:
Substituindo os termos pelos dados obtidos, temos:
Com a vazão mássica, podemos calcular a taxa de transferência de calor usando a seguinte equação:
Substituindo os termos pelos dados obtidos, temos:
Passo 7
Agora, queremos encontrar o número de Nusselt, para isso, vamos precisar calcular a seguinte proporção . Assim temos:
O número de Nusselt é determinado na Tabela 8-4 por meio de interpolação linear para proporção de e . Assim obtemos que .
Então o coeficiente de transferência de calor na superfície interna do tubo anular pode ser determinado da seguinte maneira:
Substituindo os termos pelos dados obtidos, temos:
Passo 8
Podemos determinar o comprimento do tubo com a equação para transferência de calor. Assim temos:
Aqui, é a temperatura média logarítmica, é o coeficiente de transferência de calor na superfície interna do tubo, é a taxa de transferência de calor e é a área da superfície interna do tubo .
Substituindo os termos pelos dados obtidos, temos:
Aqui, o comprimento do tubo é menor que o comprimento da entrada do limite térmico . Portanto, o comprimento do tubo deve ser maior para que o fluxo seja totalmente desenvolvido.