Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 11.Exercício - Ex. 17

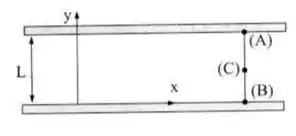
A função de corrente de um escoamento plano de um fluido incompressível, entre duas placas infinitas, paralelas é dada por:

Ψ = v 0 2 L y 2

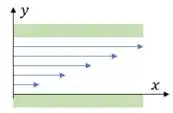
  1. Determinar o diagrama de velocidades e representa-lo graficamente
  2. Verificar se o escoamento é possível
  3. O movimento é variado ou permanente?
  4. O movimento é rotacional ou irrotacional?
  5. Determinar a cota do ponto (C) que divide a seção (A) e (B) em duas seções (AC) e (CB) de mesma vazão.

Passo 1

Item A)

Pelas equações 11.32 podemos dizer:

v x = ∂ Ψ ∂ y     e     v y = - ∂ Ψ ∂ x

A velocidade em x:

v x = ∂ ∂ y v 0 2 L y 2  

v x = v 0 L y  

A velocidade em y:

v y = - ∂ ∂ x v 0 2 L y 2

v y = 0

Passo 2

Item B)

A questão afirma que o fluido é incompressível. Para que isso seja verdade o divergente da velocidade vetorial deve ser igual a zero:

d i v   v → = ∂ v x ∂ x + ∂ v y ∂ y

d i v   v → = ∂ v 0 L y   ∂ x + ∂ ( 0 ) ∂ y

d i v   v → = 0 + 0

d i v   v → = 0

O divergente é zero, então este escoamento é possível.

Passo 3

Item C)

Em escoamento permanente não é acelerado ao longo do tempo. Em outras palavras, para um escoamento ser permanente a derivada temporal da velocidade deve ser zero:

∂ v → d t = ∂ v x ∂ t + ∂ v y ∂ t

∂ v → d t = ∂ v 0 L y ∂ t + ∂ ( 0 ) ∂ t

∂ v → d t = 0 + 0

∂ v → d t = 0

Logo, o escoamento é permanente.

Passo 4

Item D)

A rotacionalidade de um escoamento unidimensional é dada por:

r o t   v → = ∂ v y ∂ x - ∂ v x ∂ y e → z  

r o t   v → = ∂ ( 0 ) ∂ x - ∂ v 0 L y ∂ y e → z  

r o t   v → = - ∂ v 0 L y ∂ y ⋅ e → z  

r o t   v → = - v 0 L ⋅ e → z  

A rotacionalidade é diferente de zero, logo este é um escoamento rotacional.

Passo 5

Item E)

Para que a região AC e CB sejam iguais, é necessário suas integrais sejam iguais da seguinte maneira:

∫ B C v x d A = ∫ C A v x d A

A área é a base das placas vezes a altura y:

∫ B C v x ⋅ b d y = ∫ C A v x ⋅ b d y

Já os limites variam entre 0 na região (B), uma altura y que queremos descobrir em (C) e a altura máxima L em (A)

∫ 0 y v x ⋅ b d y = ∫ y L v x ⋅ b d y

∫ 0 y v 0 L y ⋅ b d y = ∫ y L v 0 L y ⋅ b d y

∫ 0 y y ⋅ d y = ∫ y L y ⋅ d y

y 2 2 0 y = y 2 2 y L

y 2 2 = L 2 2 - y 2 2

y 2 = L 2 2

y = 2 2 L

Resposta

  1. v x = v 0 L y  
  2. escoamento é possível
  3. escoamento é permanente
  4. escoamento rotacional.
  5. y = 2 2 L
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A componente de velocidade u de um campo de escoamento permanente, bidimensional, incompressível é u =a x 2 -b x y , onde a e b são constantes. A componente de velocidade v é desconhecida. Encontre um
Um bloco desliza para baixo em uma parede longa, reta, inclinada, com a velocidade V , sobre um filme fino de óleo de espessura h (Figura P9-113).O peso do bloco é W ,e sua área de contato com a filme
Considere o seguinte escoamento incompressível bidimensional, que claramente satisfaz a continuidade: u = U 0 = c o n s t a n t e ,v = V 0 = c o n s t a n t e Encontre a função corrente ψ ( r , θ ) pa
Considere o potencial de velocidade incompressível bidimensional ϕ = x y + x 2 - y 2 . (a) É verdade que ∇ 2 ϕ = 0 , e, em caso afirmativo, o que isso significa? (b) Se ela existe, encontre a função c
Um campo de escoamento incompressível bidimensional é definido pelos componentes de velocidade u = 2 V x L - y Lv = - 2 V y L em que V e L são constantes. Se elas existem, encontre a função corrente e