Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 61

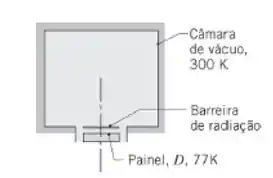
No fundo de uma grande câmara de vácuo cujas paredes estão a 300 K, um painel negro com 0,1 m de diâmetro é mantido a 77 K. Para reduzir o calor ganho nesse painel, uma barreira de radiação com o mesmo diâmetro D e uma emissividade de 0,05 é colocada muito próxima ao painel. Calcule o ganho de calor líquido no painel.

Passo 1

Vamos lá! O que queremos aqui é descobrir a taxa de calor, q 1 , que consegue atravessar a barreira e chegar no painel!

q 1 = E b 2 - E b 1 R

Pra visualizar melhor o que esta acontecendo, vamos desenhar um esquema da resistência do nosso sistema:

Somando as resistências, temos:

R = 1 - ε 2 A 2 ε 2 + 1 A 2 F 2 s + 1 - ε s A s ε s + 1 - ε s A s ε s + 1 A s F s 1 + 1 - ε 1 A 1 ε 1

Mas a área superfícial do interior da camara, A 2 é muuito maior do que a área da superfície da barreira, A s e do painel, A 1 , então podemos considerar:

1 - ε 2 A 2 ε 2 = 0

O enunciado diz que o painel é negro, logo, ε 1 = 0 , com isso:

1 - ε 1 A 1 ε 1 = 0

Usando a regra da reciprocidade:

A 2 F 2 s = A s F s 2

E considerando F s 1 = F s 2 = 1 , ficamos com:

R = 1 - ε s A s ε s + 1 - ε s A s ε s + 1 A s + 1 A s = 2 1 - ε s A s ε s + 2 A s

Passo 2

Voltando a q 1 :

q 1 = E b 2 - E b 1 R = σ T 2 4 - T 1 4 R

Substituindo R :

q 1 = σ T 2 4 - T 1 4 2 1 - ε s A s ε s + 2 A s

Podemos isolar a área e como A s = A 1

q 1 = A 1 σ T 2 4 - T 1 4 2 1 - ε s ε s + 2

O enunciado diz que:

D 1 = 0,1   m

ε S = 0,05

T 2 = 300   K

T 1 = 77   K

Lembrando que σ = 5,67 × 10 - 8 W / m 2 K 4 , podemos substituir:

q 1 = π 0,1 2 4 × 5,67 × 10 - 8 300 4 - 77 4   2 1 - 0,05 0,05 + 2

q 1 = 89,9 × 10 - 3 W

Uhuuuul!!

Resposta

q 1 = 89,9 × 10 - 3 W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o cilindro circular de diâmetro D, comprimento L e áreas A1, A2 e A3, representando as superfícies da base, interna e superior, respectivamente.(a) Mostre que o fator de forma entre a base d
Considere os planos paralelos, com extensão infinita na direção normal à página, que têm arestas opostas alinhadas conforme mostrado na figura.(a) Usando relações apropriadas do fator de forma e resul
Determine o fator de forma, F 12 , para os retângulos mostrados nas figuras.
Uma pista de patinação no gelo circular com 25m de diâmetro encontra-se coberta por uma cúpula hemisférica com 35m de diâmetro. Se as superfícies do gelo e da cúpula puderem ser aproximadas por corpos
Um forno de secagem é constituído por um longo duto semicircular com diâmetro D=1m . Os materiais a serem secados cobrem a base do forno, enquanto a parede é mantida a 1200K . Qual é a taxa de secagem