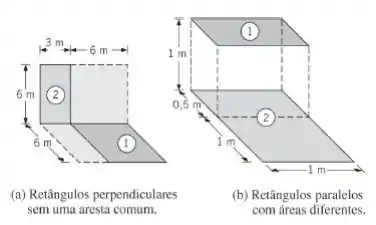
Determine o fator de forma, , para os retângulos mostrados nas figuras.

Para resolver essa questão vamos assumir comportamento difuso da superfície. Definindo as superfícies hipotéticas e , como as partes que se completam da figura da letra (a) sendo a ao lado de e a ao lado da . A partir da regra do fator de exibição aditiva podemos escrever:

Observe com cuidado quais fatores podem ser avaliados na Fig. 13.6 para retângulos perpendiculares com uma aresta comum. Da simetria temos que:

Usando reciprocidade,

Então,

Resolvendo a primeira equação do Passo 2 para e substituindo na equação anterior para , temos que:

Avaliando os fatores de forma da Fig. 13.6:

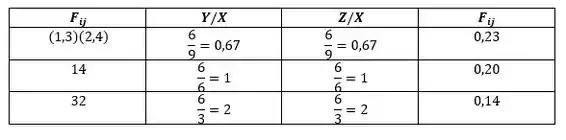
Substituindo os valores numéricos temos:

Agora vamos pegar as superfícies que chamamos de e dividir em duas seções, e . A partir da regra do fator de exibição aditiva, temos:

Os fatores de forma podem ser avaliados na Fig. 13.4 para retângulos paralelos alinhados. Para avaliar , primeiro reconhecemos que um relacionamento envolvendo será necessário. Usando a regra aditiva novamente,

Observe que, por considerações de simetria,

E usando reciprocidade temos:

Então,

Logo temos que,

E resolvendo para , notando que e

Avaliando os fatores de forma da Fig. 13.4:

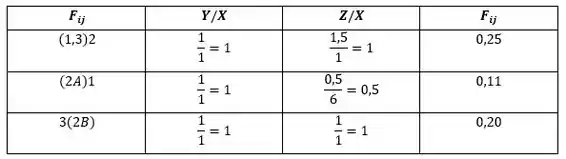
Substituindo os valores numéricos temos: