Considere o sótão de uma casa localizada em um local de clima quente. O piso do sótão é caracterizado por uma largura = 10 m, enquanto o telhado faz um ângulo de θ = 30° a partir da direção horizontal, como mostrado na figura. O proprietário quer reduzir a carga térmica para a casa através da cola de um filme de alumínio brilhante (εf = 0,07) sobre as superfícies do espaço do sótão. Antes da instalação do filme, as superfícies tinham uma emissividade de = 0,85.

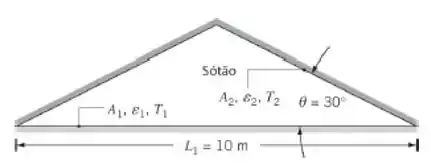
1. Considere a instalação somente na superfície inferior do telhado do sótão. Determine a razão entre as transferências de calor radiantes após e antes da instalação do filme.
2. Determine a razão entre as transferências de calor radiantes após e antes da instalação se o filme for instalado somente sobre o piso do sótão.
3. Determine a razão entre as transferências de calor radiantes se o filme for instalado sobre o piso do sótão e na parte inferior do telhado.

Antes da instalação temos:

A transferência de calor radiante é dada por:

A razão entre as trasferências de calor radiante pode ser calculada:

Simplificando, ficamos com:

Substituindo as áreas e o fator de forma:

Agora a gente só precisa substituir e para cada situação!

Primeiro o alumínio é instalado apenas no telhado, então, e , substituindo:

Calculando:

Agora o alumínio é instalado apenas no telhado, então, e e, substituindo:

Calculando:

Por fim, o alumínio é instalado nas duas superfícies,então, e e, substituindo:

Temos:

Uhuuuul!!!