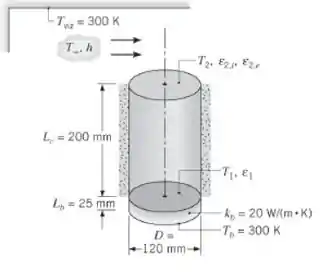
Discos metálicos revestidos são curados colocando-os na parte superior de um forno cilíndrico cuja superfície inferior (base) é eletricamente aquecida e cuja parede lateral pode ser aproximada por uma superfície rerradiante. O processo de cura é obtido pela manutenção do disco a por um longo período de tempo. A superfície eletricamente aquecida é mantida a e está montada sobre uma base de material cerâmico com condutividade térmica . A superfície inferior do material da base, assim como o ar ambiente e a grande vizinhança acima do disco, são mantidos a uma temperatura de 300 K. As emissividades da superfície do aquecedor e das superfícies interna e externa do disco são e , respectivamente. Supondo operação em regime estacionário e desprezando a convecção no interior da cavidade cilíndrica, determine a potência elétrica que deve ser fornecida ao aquecedor e o coeficiente de transferência de calor por convecção h que deve ser mantido na superfície externa do disco, com o objetivo de satisfazer as condições especificadas.
Passo 1
Shoow de bola galerinhaaa !!
Vamos continuar?
Antes de qualquer coisa vamos desenhar as resistências:
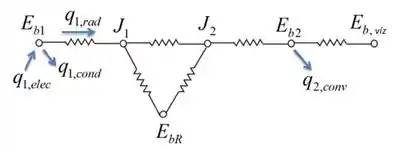
Bom galera, nós queremos achar a potência elétrica que deve ser fornecida ao aquecedor e o coeficiente de transferência de calor por convecção h que deve ser mantido na superfície externa do disco , certo?
Bom, pelo desenho nós já podemos perceber que a superfície 1 está recebendo calor por eletricidade e perdendo por radiação e convecção, ou seja:
O calor condutivo nós sabemos calcular:
Quando nós temos três superfícies com uma superfície sendo rerradiante podemos usar a fórmula:
Então:
As potências emissivas nós sabemos calcular, não é?
Substituindo:
Vamos ver o que sabemos?
A área nós também sabemos, não é?
Achamos quase tudo, mas ainda não temos os fatores de forma!!
Passo 2
Olhando a figura abaixo para os discos coaxiais:
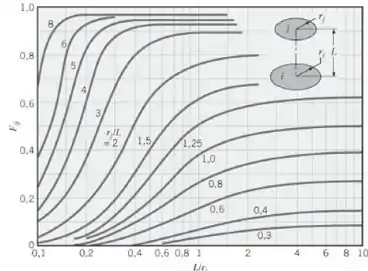
Sabendo que:
Então:
Olhando no gráfico:
Pela reciprocidade:
Aplicando a soma para a superfície 1:
Então agora é só substituir:
Achamos a potência elétrica a ser fornecida, não é?
Passo 3
Agora nós ainda temos que achar o coeficiente convectivo !!
Fazendo o balanço no disco:
Substituindo:
Colocando nossos valores:
E é isso aí galerinha, bora seguir ??