Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 7

Considere o cilindro circular de diâmetro D, comprimento L e áreas A1, A2 e A3, representando as superfícies da base, interna e superior, respectivamente.

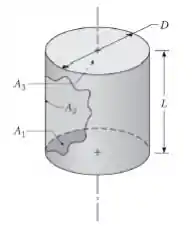
(a) Mostre que o fator de forma entre a base do cilindro e sua superfície interna tem a forma F 12 =   2 H 1   +   H 2 1 2   –   H , com H   = L D .

(b) Mostre que o fator de forma da superfície interna para ela mesma tem a forma F 22   =   1   1   H   –   1   +   H 2 1 2 .

Passo 1

Fala aiiii, tudo bem? Nessa questão nós temos um cilindro circular de diâmetro D , comprimento L e as áreas A 1 ,   A 2 e A 3 representando a base, as superfícies laterais e superiores, respectivamente.

Com essas informações vamos mostrar que o fator de visão entre a base do cilindro e a superfície lateral interna tem a forma:

F 12 =   2 H 1   +   H 2 1 2   –   H

Com,

H   = L D

E que o fator de forma da superfície interna para ela mesma tem a forma :

F 22   =   1   1   H   –   1   +   H 2 1 2

Passo 2

Para resolver essa questão vamos assumir superfícies difusas com radiosidades uniformes.

A relação para F 12 , superfície lateral base-interior aplica-se a regra de soma a A 1 , observando que F 11   =   0 .

F 11 + F 1 2 + F 1 3 = 0  

F 1 2 = 1 - F 1 3      

Na Tabela 13.2, Fig. 13.5, com i   =   1 ,     j   =   3 ,

F 13 = 1 2 S - S 2 - 4 D 3 D 1 2 1 2

s = 1 + 1 + R 3 2 R 1 2 = 1 R 2 + 2 = 4 H 2 + 2

Onde R 1 =   R 3   =   R   = D 2 L e H   = L D .

Com isso encontramos:

F 12 =   1 - 1 2 4 H 2 + 2 - 4 H 2 + 2 2   – 4 1 2

F 12 =   2 H 1   +   H 2 1 2   –   H

Passo 3

A relação para F 22 , superfície lateral interna aplicando a regra de soma em A 2 e reconhecendo que F 23 =   F 21 ,

F 21 + F 2 2 + F 2 3 = 1

F 2 2 = 1 - F 21

Usando a reciprocidade entre A 1 e A 2 ,

F 21 = A 1 A 2 F 12

Usando as expressões de área,

F 22 = 1 - 2 A 1 A 2 F 12 = 1 - 2 D 4 L F 12 = 1 - 1 2 H F 12

Onde A 1 = π D 2 4 e A 2 = π D L .

Substituindo a equação encontrada na letra (a) para F 12 , encontramos:

F 22   =   1 - 1 2 H 2 H 1   +   H 2 1 2 - H =   1 + H   –   1   +   H 2 1 2

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma ferramenta para o processamento de pastilhas de silício está posicionada no interior de uma câmara de vácuo cujas paredes são negras e mantidas a T c v=300K , por um refrigerante. A fina pastilha
Seja o Problema 6.17. A placa estacionária, o ar ambiente e a vizinhança estão a T ∞ = v i z=20 ° C . Sendo a temperatura do disco em rotação de T s = 80 ° C , qual é a potência total dissipada a part
A maioria dos arquitetos sabe que o teto de uma pista de patinação no gelo tem que ter uma alta refletividade. Caso contrário pode ocorrer condensação no teto e a água pingar sobre o gelo, causando ca
Considere duas placas paralelas muito grandes. A placa inferior é mais quente do que a superior, que é mantida a uma temperatura constante de T 1 =330K . As placas estão separadas por L = 0,1 m e no e
Discos metálicos revestidos são curados colocando-os na parte superior de um forno cilíndrico cuja superfície inferior (base) é eletricamente aquecida e cuja parede lateral pode ser aproximada por uma