Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 5.Problemas - Ex. 19

A parede plana de uma fornalha é fabricada em aço-carbono não ligado ( k = 60 W / ( m . K ) , ρ = 7850   k g / m 3 , c = 430 J / ( k g . K ) ) e tem uma espessura L = 1 5 m m . Para proteger essa parede dos efeitos corrosivos dos gases de combustão, uma superfície da parede é revestida por uma fina película cerâmica que, para uma unidade de áre superficial, tem uma resistência térmica de R t , f ' ' = 0,001   m 2 . K / W . A superfície oposta encontra-se termicamente isolada da vizinhança.

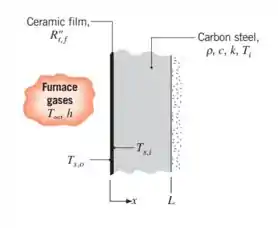
Na partida da fornalha, a parede se encontra a uma temperatura inicial de T i = 300 K e gases de combustão, a T ∞ = 1300 K , entram na fornalha, mantendo na película cerâmica um coeficiente convectivo h = 30 W / ( m 2 . K ) . Supondo que a película tem uma capacitância térmica desprezível, quanto tempo irá levar até que a superfície interna do aço atinja uma temperatura de T s , i = 1 0 00 K ? Neste instante, qual é a temperatura T s , e na superfície externa da película cerâmica?

Passo 1

Faaalaaa coleguinhaa... Bora de mais transferência de calor!!

Bom, vamos começar encontrando o coeficiente global de transferência de calor, ele pode ser encontrado somando-se as resistências, lembre-se que temos uma resistência convectiva, então precisamos do h (felizmente o exercício deu esse carinha) e o enunciado nos deu mais uma resistência ali da película, que representa a condução. Então teremos o seguinte:

U = 1 1 h + R t , f ' ' = 1 1 30 + 0,001 = 28,30 W / m 2 . K

Beleza, então se tivermos um B i < 0,1 podemos trabalhar com o método da capacitância pode blocos:

B i = U L k = 28,30 0 , 0 15 60 = 0,0 0 7075 < 0,1

É isso mesmo. Só tacar-lhe o pau nesse carrinho!!

Passo 2

Lembra da relação??

θ = T - T ∞ T i - T ∞ = e t R C = e - U t ρ L c

Se passarmos ln nos dois lados:

ln ⁡ T - T ∞ T i - T ∞ = - U t ρ L c

Então:

t = - ρ L c U ln ⁡ T - T ∞ T i - T ∞ = - 7850 0,015 430 28,80 ln ⁡ 300 1000

Logo,

t = 2116,67 s e g → h = 0,6 h o r a s

Passo 3

Ta comigo?? Ainda falta um último passo, bem tranquilo, a única coisa que o exercício pede é a temperatura na outra face.

Bom, sabemos que as taxas de transferências de energia condutiva e convectiva são iguais certo? Teremos então:

q ˙ c o n v = q ˙ c o n d

Ou seja:

h T ∞ - T s , o = T s , o - T s , i R t , f ' '

Lembrando que queremos a temperatura na superfície externa, então basta isolar T s , o :

T s , o = h T ∞ + T s , i R t , f ' ' h + 1 R t , f ' '

Ou seja:

T s , o = 1069,23 K

Muuitoo que beee! Só riscar mais uma e partir pra próxima!!

Resposta

Portanto:

  1. t = 2116,67 s e g
  2. T s , o = 1069,23 K
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

À medida que as estações espaciais permanentes aumentam de tamanho, existe um consequente aumento na quantidade de potência elétrica que elas dissipam. Para manter a temperatura nos compartimentos int
Como observado no Problema 5.3, fornos de micro-ondas operam alinhando e revertendo moléculas de água no interior do alimento, resultando em geração volumétrica de energia e, desta maneira, no cozimen
No armazenamento termomecânico de dados, uma cabeça de processamento, constituída por M pontas aquecidas, é usada para escrever os dados sobre um meio polimérico de armazenamento. Há microaquecedores
O derretimento da água inicialmente na temperatura de fusão, Tf = 0°C, foi considerado no Exemplo 1.6. O congelamento da água frequentemente ocorre a 0°C. Contudo, líquidos puros, que passam por um pr
O objetivo desse problema é desenvolver modelos térmicos para estimar temperaturas no regime estacionário e o histórico das temperaturas transientes do transformador elétrico mostrado a seguir.A geome