O dissipador de calor do Problema 7.29 é considerado para uma aplicação na qual a dissipação de potência é de apenas 70W e o engenheiro propõe o uso no resfriamento de ar a T„= 20°C. Se a temperatura da base tem que permanecer abaixo de 70°C, qual velocidade do ar é necessária? As propriedades do ar podem ser aproximadas por k = 0,027 W/(m-K), v = 16,4 X 10~ 6 m’ /s e Pr = 0,706. Sugestão: Há necessidade de uma solução iterativa. Uma abordagem é considerar que a eficiência das aletas seja igual a um para iniciar as iterações.
Passo 1
Fala aí galerinha? Tudo bem com vocês? Bora pra cima! Do circuito térmico:
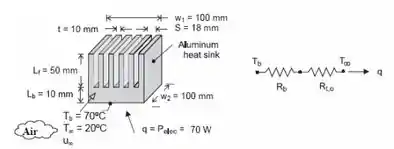
Temos que:
Das equs 3.102 e 3.103:
Dessa forma,
![]()
Como é a incógnita na expressão para , as equações anteriores podem ser resolvidas com duas variáveis e .
Passo 2
Dessa forma, podemos agora proceder para encontrar a velocidade para o coeficiente de transferência de calor.
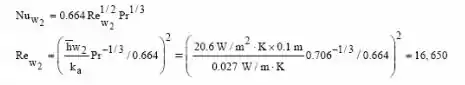
Assumindo que o fluxo laminar está correto, logo,