Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 9.Problemas - Ex. 1

Um gás ideal escoa adiabaticamente através de um tubo. Na seção 1, p 1 = 140   k P a , T 1 = 260 ° C e V 1 = 75   m / s . Mas a jusante, p 2 = 30   k P a , T 1 = 207 ° C . Calcule a velocidade V 2 em m/s e s 2 - s 1 em J / ( k g ; k ) se o gás for (a) ar, k = 1,4 e (b) argônio, k = 1,67 .

Passo 1

E aí, galeraaaa! Tudo bem? Animados para mais um exercício de mecflu?

Como de costume, eu vou te convidar a desenhar antes de mais nada o problema comigo, beleza?

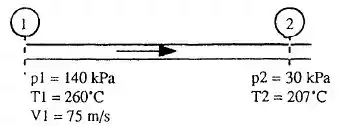
Passo 2

(a) Vamos usar então a equação de energia para um escoamento estacionário para resolver esse problema aqui, beleza? Essa equação no livro é a 9.23!!!

C p T 1 + 1 2 V 1 2 = C p T 2 + 1 2 V 2 2

Da tabela A.2 do livro a gente obtém que C p = 1005   J / ( k g . k ) , então fica molezinha a gente descobrir quem é nossa velocidade V2, certo?

1005 260 + 1 2 75 2 = 1005 207 + 1 2 V 2 → V 2 = 335   m / s

IMPORTANTE: Note que apesar de J ter unidade em K (kelvin), você pode usar na sua equação acima a temperatura em °C, uma vez que a variação de 1°C equivale a 1K. Mas mais importante do que isso é também verificar que a equação é linear em T, porque se ali na temperatura tivesse um expoente qualquer que seja, a temperatura necessariamente deveria ser colocada em Kelvin.

Passo 3

Agora vamos partir para calcular nossa variação de entropia. O livro já deu pra gente como é essa equação, beleza? Também na tabela A-2 você vai ver que pro ar R = 287 J/kg.K

s 2 - s 1 = C p ln ⁡ T 2 T 1 - R l n p 2 p 1 = 1005 ln ⁡ 207 + 273 260 + 273 - 287 ln ⁡ 30 140 = 337   J / ( k g . K )

Importante você ter em mente que ao utilizar essa equação você estará considerando gás ideal!!! Então se for usar isso na sua prova, é sempre bom deixar claro pro professor saber que tu manja dos paranauês termodinâmicos também, além de mecflu 😉

Passo 4

(b) Para o argônio é só a gente seguir a mesma lógica que usamos para o ar, primeiro fazemos a equação de energia e depois a de entropia e entramos com os valores. Na tabela A-4 do livro você vai ver que C p = 518   J / ( k g . k ) e R = 208 J/kg.K para o argônio.

C p T 1 + 1 2 V 1 2 = C p T 2 + 1 2 V 2 2

518 260 + 1 2 75 2 = 518 207 + 1 2 V 2 2 → V 2 = 246   m / s

s 2 - s 1 = C p ln ⁡ T 2 T 1 - R l n p 2 p 1

s 2 - s 1 = 518 ln ⁡ 207 + 273 260 + 273 - 208 ln ⁡ 30 140 = 266   J / ( k g . k )

Resposta

a V 2 = 335 m s                 s 2 - s 1 = 337 J k g . K

( b ) V 2 = 246 m s                 s 2 - s 1 = 266 J k g . K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ar escoa por um duto de área variável. Na seção 1, A 1 = 20c m ² ², p 1 = 300k P a , ρ 1 = 1,75k g / m ³ ³ e V 1 = 122,5m / s . Na seção 2, a área é exatamente a mesma, mas a massa específica é bem me
Se 8 kg de oxigênio em um tanque fechado a 200°C e 300 kPa é aquecido até que a pressão aumente para 400 kPa, calcule (a) a nova temperatura, (b) a transferência de calor total e (c) a variação na ent
Em muitos problemas, as propriedades sônicas (*) são valores de referência mais convenientes que as propriedades de estagnação. Para escoamento isentrópico de um gás perfeito, deduza relações para p/p
C O 2 expande isentropicamente, por um duto, de p 1 = 125k P a e T 1 = 100 ° C para p 2 = 80k P a e V 2 = 325m / s . Calcule (a) T 2 , (b) M a 2 , (c) T 0 , (d) p 0 , (e) V 1 e (f) M a 1 .