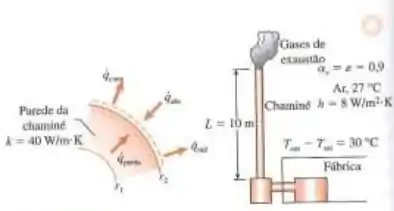
Gases de exaustão de uma fábrica estão sendo expelidos pela chaminé de exaustão de 10 m de altura, 1 m de diâmetro externo, 10 cm de espessura da parede e condutividade térmica de . Os gases de exaustão são descarregados a uma taxa de 1,2 kg/s, enquanto a queda de temperatura entre a entrada e saída do gás na chaminé é de 30 °C, e o calor específico e a pressão constante dos gases de exaustão é . Em um determinado dia, a superfície externa da chaminé é sujeita à radiação na área circundante a 27 °C e convecção no ar ambiente a 27 °C, com coeficiente médio de transferência de calor por convecção de . A radiação solar incidente sobre a superfície externa da chaminé é de , e a emissividade e absortividade solar da superfície externa são, ambas, 0,9. Assumindo a transferência de calor unidimensional em regime, (a) obtenha a variação de temperatura na parede da chaminé e (b) determine a temperatura da superfície interna da chaminé.

O nosso primeiro passo é fazer considerações para resolver o nosso problema. Sendo assim, temos um problema de regime permanente, sem geração de calor e condutividade térmica constante. Além disto, é importante destacarmos o fato de ser condução unidimensional. Isto é, não irá variar a temperatura de acordo com a altura da chaminé!

Então, para resolvermos a letra a) precisamos determinar a equação diferencial do nosso problema e as duas condições de contorno.

Portanto, devido as restrições do problema, temos a seguinte equação diferencial:

Já a condição de contorno que temos é na superfície interna da chaminé, a qual é dada por:

E só temos esta restrição. Como a nossa EDO é de segunda ordem, precisamos de duas restrições. E aí? Nosso primeiro trabalho é descobrirmos quem é essa segunda restrição (e calcularmos esse .

Começando por , ele é exatamente o calor cedido pela queda de temperatura dos gases de exaustão. Portanto,

E agora, a nossa segunda condição de contorno? Ela será a temperatura no raio externo da chaminé. Para obtermos ela, será necessário fazermos um balanço de energia na chaminé, considerando os efeitos de condução, convecção e radiação! Sendo assim, temos:

Substituindo os valores, temos:

E então, o problema é resolver a equação acima. Não conseguimos resolver analiticamente, somente através de métodos numéricos ou plotando o gráfico da função. Resolvendo por qualquer um destes métodos, vamos obter que:

E esta é a nossa segunda condição de contorno!