Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 33
Glicerina a 15 °C escoa entre placas paralelas com espaçamento entre elas. A placa superior move com velocidade no sentido positivo de . O gradiente de pressão é . Localize o ponto de velocidade máxima e determine o seu módulo (faça na placa inferior). Determine o volume de glicerina (m³) que passa por uma dada seção transversal (x = constante) em 10 s. Trace gráficos das distribuições de velocidade e de tensão de cisalhamento.
Passo 1
Tá legal! A primeira coisa que devemos fazer é escrever a equação para o perfil de velocidade nesse caso, que será dado pela equação 8.8 vista nessa seção do livro, então, teremos:
Então para obter a velocidade máxima, devemos derivar a expressão da velocidade e igualar ela a zero, então, teremos:
Então, a posição em que isso ocorre será:
Então, para encontrar seu valor, devemos buscar o valor da viscosidade nas tabelas do apêndice A, então, para glicerina a 15 °C, temos:
Então, substituindo os valores conhecidos na equação acima, temos:
Passo 2
Dessa forma, a velocidade máxima então, será:
Substituindo os valores conhecidos, temos:
Passo 3
Agora, para encontrar o volume de glicerina que passa por uma dada seção transversal, vamos utilizar a equação da definição da vazão, dada por:
Então, colocando no formato pedido no enunciado, para uma dada seção transversal, teremos:
Agora, substituindo a expressão para a velocidade, temos:
Então, resolvendo essa integral, chegamos em:
Substituindo os limites de integração, temos:
Substituindo os valores conhecidos, teremos a vazão para uma seção transversal:
Então, o volume que vai passar por essa seção em será dado por:
Passo 4
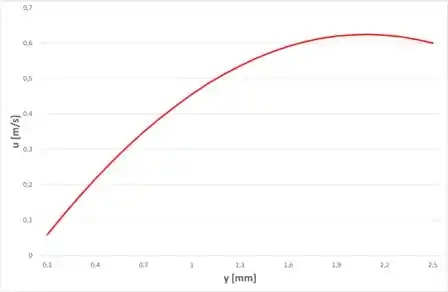
Agora, vamos plotar o gráfico da distribuição de velocidade em função de , então, com o auxílio da equação de velocidade do passo 1, descrita a seguir, temos:
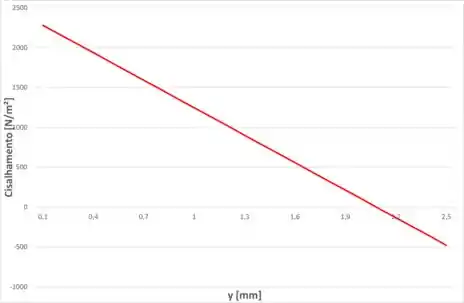
E, agora, para a tensão de cisalhamento, temos:
Então, teremos:
E o gráfico dessa equação será:
