Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 40
A eficiência da bomba de arrasto viscoso da Fig. P8.39 é dada por
Em que é uma vazão adimensional (Q é a vazão volumétrica para o diferencial de pressão , e é a profundidade normal ao diagrama). Trace um gráfico da eficiência versus a vazão adimensional e determine a vazão para a eficiência máxima. Explique porque a eficiência tem picos e porque ela é zero para certos valores de .
Passo 1
Beleza! A primeira coisa que vamos fazer aqui é desenhar o gráfico da eficiência pela vazão adimensional, então, a equação:
Irá gerar o seguinte gráfico:
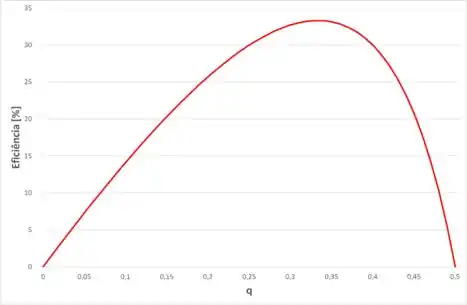
Passo 2
A eficiência máxima pode ser encontrada através do próprio gráfico, através dele então, temos que:
E, para essa eficiência, a vazão adimensional será:
Passo 3
Tá legal, agora vamos analisar o comportamento da curva de eficiência em função da vazão adimensional. Nesse caso, temos que a eficiência é zero para a vazão adimensional zero pois nesse ponto não há vazão alguma passando pela bomba. Ela será zero novamente quando a vazão é máxima, uma vez que a potência é dada por:
Quando temos vazão máxima, a nossa queda de pressão será zero, então a potência será zero e por consequência a eficiência também. E o pico de eficiência se dá no intervalo entre esses dois pontos, onde se encontra o equilíbrio entre a vazão e a queda de pressão.