Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 9.Exercício - Ex. 8

Uma gota de chuva tem diâmetro médio de 2,5   m m . Calcular a velocidade limite da gota se o ar tem ρ = 1,2   k g / m 3 e ν = 1,8 ⋅ 10 - 6 m 2 / s

Passo 1

A situação de uma gota caindo pode ser resumida na imagem abaixo

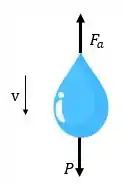
Quando a velocidade máxima v é atingida, não existe aceleração resultante sobre a gota, então podemos dizer que a força de arrasto é igual a força peso:

F a = P

Substituíndo o equação da força de arrasto e da força peso temos:

C a ⋅ ρ a r ⋅ v 2 ⋅ A g o t a 2 = ρ a g u a ⋅ g ⋅ V g o t a

Isolando a velocidade:

v = 2 ⋅ ρ a g u a ⋅ g ⋅ V g o t a C a ⋅ ρ a r ⋅ A g o t a

Mas para determinar o valor da velocidade precisamos calcular a área e o volume da gota e o coeficiente de arrasto.

Passo 2

Se considerarmos que a gota é perfeitamente esférica, a área de referência e o volume são dados por:

A g o t a = π D 2 4 = π ⋅ 2,5 ⋅ 10 - 3 2 4 = 4,91 ⋅ 10 - 6   m 2

V g o t a = 1 6 π D 3 = π ⋅ 2,5 ⋅ 10 - 3 3 6 = 8,18 ⋅ 10 - 9   m 3

Passo 3

Como a gota se encontra em velocidade máxima, então podemos assumir que o valor do número de Reynolds seja em torno de: 1000 < R e < 3,5 ⋅ 10 5 . Nessas condições, o coeficiente de arrasto é constante e igual a:

C a = 0,45

Passo 4

Agora podemos calcular a velocidade da gota:

v = 2 ⋅ ρ a g u a ⋅ g ⋅ V g o t a C a ⋅ ρ a r ⋅ A g o t a

v = 2 ⋅ 1000 k g m 3 ⋅ 10 m s   ⋅ 8,18 ⋅ 10 - 9   m 3 0,45 ⋅ 1,2 k g m 3 ⋅ 4,91 ⋅ 10 - 6   m 2

v = 7,85 m s

Passo 5

Agora, vamos calcular o número de Reynolds para garantir que nossa hipótese está correta:

R e = v ⋅ D ν

R e = 7,85 m s ⋅ 2,5 ⋅ 10 - 3 1,8 ⋅ 10 - 6 m 2 / s

R e = 0,109 ⋅ 10 5

Assim confirmamos que o número de Reynolds está no intervalo 1000 < R e < 3,5 ⋅ 10 5 , confirmando a validade da nossa hipótese.

Resposta

v = 7,85 m s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dados balísticos, obtidos de uma bancada de tiro, mostram que o arrasto aerodinâmico reduz a velocidade de uma bala de revólver magnum .44 de 250 m/s para 210 m/s, em um trajeto horizontal de 150 m. O
Foi proposta a utilização de tambores excedentes de óleo de 208 litros para fazer moinhos de vento simples em países subdesenvolvidos. (É uma turbina tipo Savonius simples). Duas configurações possíve
Aantenadeumcarrotem10mmdediâmetroe1,8mdecomprimento.Estimeomomentofletorquetendeaarrancá­la,seo carroforconduzidoa120km/hemumdia­padrão.
Comparedetraceumgráficodapotência(kW)requeridaporumsedanamericanogrande,típicodadécadade1970,eporum atualsedandetamanhomédioparasuperaroarrastoaerodinâmico,emfunçãodavelocidadenoar­padrão,paraafaixade
A resistência ao movimento de uma boa bicicleta sobre um pavimento liso é decorrente, quase que inteiramente, do arrasto aerodinâmico. Considere que a massa total de ciclista e bicicleta é W = 100 kg.