Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 5.Exercício - Ex. 1

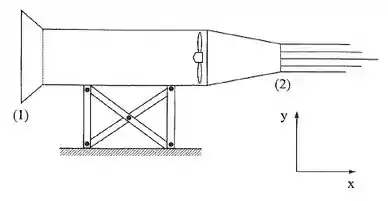
Calcular o esforço horizontal sobre a estrutura do ventilador da figura e a potência transmitida ao fluido pelo ventilador. Desprezar a perda de carga entre as seções (1) e (2). Dados: D 2 = 0,38   m ; v 2 = 30   m / s ; γ - 12,7   N / m 3 ; v 1 ≅ 0 .

Passo 1

A equação que representa a força que o fluido exerce é dada por:

F → s = - p 1 A 1 n → 1 + p 2 A 2 n → 2 + Q m v → 2 - v → 1

Através do desenho, podemos ver que a pressão nos pontos 1 e 2 é igual a zero, o que anula os dois primeiros termos, e o enunciado nos disse também que v 1 ≅ 0 . Como o escoamento se dá somente na direção x , temos:

F → s = - Q m v → 2 → F s x = - ρ v 2 2 A 2 = - γ g v 2 2 π D 2 2 4

Substituindo os valores conhecidos, temos:

F s x = - 12,7 9,8 30 2 π 0,35 2 4 → F s x = 132,3   N

Passo 2

Agora podemos calcular o equilíbrio de cargas entre os pontos 1 e 2:

H 1 + H B = H 2 + H p 1,2

v 1 2 2 g + p 1 γ + z 1 + H B = v 2 2 2 g + p 2 γ + z 2 + H p 1,2

Sabemos que 1 e 2 estão no mesmo nível, então z 1 = z 2 . Então, substituindo os valores conhecidos, temos:

0 2 2 10 + 0 12,7 + H B = 30 2 2 9,8 + 0 12,7 + 0 → H B = 46   m

Passo 3

Agora vamos calcular a vazão do sistema através do ponto 2:

Q = v 2 A 2 = v 2 π D 2 2 4 = 30 π 0,38 2 4 → Q = 3,4   m 3 / s

Agora podemos calcular a potência da bomba através de:

N = γ Q H B = 12,7 3,4 46 → N = 1986,3   W

Resposta

F s x = 132,3   N

N = 1986,3   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que a perda de carga no trecho (1)-(2) é 3 m, determinar as componentes horizontal e vertical da força aplicada pelo fluido nesse trecho de tubulação. Dados: γ = 10000N / m 3 ; Q = 6L / s .
A turbina da figura ‘extrai’ a potência de 2,9 kW da água em escoamento. Desprezando as perdas na redução, calcular as forças exercidas pela água sobre a redução e sobre a turbina, respectivamente. Da
A água contida no tanque (1) é descarregada através do bocal sem atrito. Seu nível h 1 pode ser considerado constante. O jato incide sobre uma placa de grandes dimensões que cobre a saída do bocal do
No esquema que segue, podem ocorrer duas situações:1) o registro (B) fechado e o registro (A) aberto, a água é despejada por (1);2) o registro (A) fechado e o registro (B) aberto, a água é despejada p
Para uma turbina de ação do tipo Pelton, tem-se os seguintes dados: raio da turbina: R = 1,5 m; rotação: 450 rpm; ângulo de saída das pás: 170°; velocidae do jato: 100 m/s; área da seção do jato: 0,1