Um grande forno convectivo-radiante é usado para tratar termicamente um pequeno produto cilíndrico com diâmetro de 25 mm e comprimento de 0,2 m. As paredes do forno são mantidas a uma temperatura uniforme de 1000 K e ar quente, a 750 K, escoa em escoamento cruzado sobre o cilindro com uma velocidade de 5 m/s. A superfície do cilindro é opaca e difusa, com a emissividade espectral mostrada na figura.

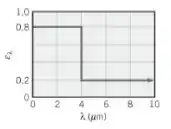
1. Determine a taxa de transferência de calor para o cilindro quando ele é colocado no forno a uma temperatura de 300 K.
2. Qual é a temperatura do cilindro em condições de regime estacionário?
3. Quanto tempo será necessário para que o cilindro atinja uma temperatura que esteja a 50°C da sua temperatura em condições de regime estacionário?

Começando pela letra a, nosso enunciado pede a taxa de transferência de calor… Podemos encontrar pela equação:

Temos algumas coisas faltando aí… Vamos começar pelo , para encontrar ele precisamos:

Vamos continuar:

E enfim teremos:

Beleza! Mas agora precisamos encontrar a emissividade…

Usando a equação 12.43, vamos nessa!

Vamos achar esse cara , para isso vamos fazer:

Visitando a tabela 12.2, vamos ter:

E nossa emissividade ficará:

Tá quase! Falta ainda achar , usando a equação 12.52, vamos lá!

Vamos achar esse novamente, porque agora nossa temperatura é diferente, vamos fazer da mesma maneira:

Visitando a tabela 12.2:

Opa! Agora podemos voltar lá:

Agora simmm!! Vamos achar a transferência de calor:

Show de bola! Partiu letra b!

Na letra b, precisamos encontrar a temperatura do cilindro, vamos usar o balanço de energia:

Tá faltando gente aí, porque agora não estamos nas mesmas condições da letra a, beleza?

Vamos começar achando o :

Vamos continuar:

E enfim teremos:

Agora encontrando a emissividade:

Vamos achar esse cara , para isso vamos fazer:

Visitando a tabela 12.2, vamos ter:

E nossa emissividade ficará:

O não vai mudar, certo? Então podemos encontrar nossa temperatura:

Uhul! Conseguimos!