Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 72

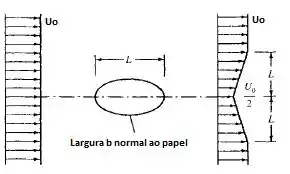
Quando imerso em uma corrente uniforme, um cilindro elíptico rombudo cria uma grande esteira a jusante, como idealizado abaixo. A pressão nas seções de montante e de jusante são aproximadamente iguais e o fluido é água a 20°C. Se U 0 = 4   m / s e L = 80   c m , calcule a força de arrasto sobre o cilindro por unidade de largura normal ao papel? Calcule também o coeficiente de arrasto adimensional C D = 2 F ρ U 0 2 b L

Passo 1

Se você já veio acompanhando esses exercícios com a gente, você vai perceber que esse exercício é MUITOOOOO parecido com o 3.34 (recomendo você dar uma olhadinha nele depois).

Vamos aplicar o mesmo volume de controle!!!

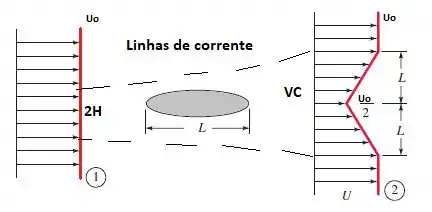
0 = ∫ ρ u d A z - ∫ ρ u d A 1 = 2 ∫ 0 L ρ U 0 2 1 + y L b d y - 2 ρ U 0 b H

Onde 2H é a altura da entrada de fluido. Se resolvermos essa igualdade para H, vamos encontrar que H = 3 L 4

Passo 2

Agora, a relação de momento linear é utilizada. Note que a força de arrasto F é para a direita, então a força que responderá a ela deve estar direcionada para a esquerda.

∑ F x = 0 = ∫ u ρ u d A z - ∫ u ρ u d A 1

∑ F x = 0 = 2 ∫ 0 L U 0 2 1 + y L ρ U 0 2 1 + y L b d y - 2 H ρ U 0 2 b = - F a r r a s t o

Lembrando que H = 3 L 4 , a força de arrasto deve ser:

F a r r a s t o = 3 2 ρ U 2 L b - 7 6 ρ U 2 L b = 1 3 ρ U 2 L b

Passo 3

Substituindo os valores, temos:

F a r r a s t o = 1 3 998 4 2 0,8 1 = 4260   N

Por fim temos que o coeficiente de arrasto será dado por: C D = 2 F ρ U 0 2 b L = 2 3

Resposta

F a r r a s t o = 4260   N                                                               C D = 2 / 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A caixa abaixo tem três orifícios de 12,5 mm do lado direito. As vazões de água a 20°C indicadas são permanentes, mas os detalhes do interior são desconhecidos. Calcule a força, se houver, que esse es
Água a 20°C descarrega para atmosfera padrão (nível do mar) através do bocal divisor abaixo. As áreas das seções são A 1 = 0,02m 2 e A 2 = A 3 = 0,008m 2 . Se p 1 = 135k P a (absoluta) e vazão é Q 2 =
Gasolina a 20°C está escoando com V 1 = 12m / s em um tubo de 5 cm de diâmetro, quando encontra um trecho de 1 m de comprimento com sucção radial uniforme na parede. No final da região de sucção, a ve
Como mostra a Figura P3.90, uma coluna líquida de altura h é confinada em um tubo vertical de seção transversal A por um tampão. Em t = 0 , o tampão é repentinamente removido, expondo o fundo do líqui
Água a 20°C escoa em regime permanente através de uma curva com redução em um tubo, como mostra a Figura P3.77. As condições conhecidas são p 1 = 350k P a , D 1 = 25c m , V 1 = 2,2m / s , p 2 = 120k P