Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 77

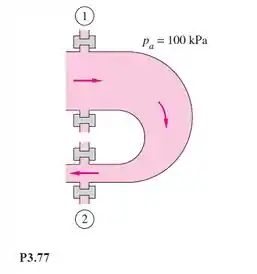
Água a 20°C escoa em regime permanente através de uma curva com redução em um tubo, como mostra a Figura P3.77. As condições conhecidas são p 1 = 350   k P a , D 1 = 25   c m , V 1 = 2,2   m / s , p 2 = 120   k P a e D 2 = 8   c m . Desprezando o peso da água e da curva, calcule a força total que deve ser suportada pelos parafusos dos flanges.

Passo 1

Vamo lá resolver essa questão!

A água flui através da curva do tubo de redução, onde parafusos de flange são usados para segurar o tubo.

Pelas propriedades da água

Densidade da água ρ = 998   k g / m 3

Aplicando o equilíbrio de forças ao longo da direção horizontal dentro do volume de controle que envolve as dobras e os cortes;

- F p a r a f u s o + p 1 g   A 1 + p 2 g A 2 = m ˙ 2 u 2 - m ˙ 1 u 1

Desde que

u 1 = V 1

u 2 = V 2

Logo

F p a r a f u s o = p 1 g   A 1 + p 2 g A 2 + m ˙ V 2 + V 1                         ( 1 )

Onde :

p 1 g é a pressão manométrica na entrada.

p 2 g é a pressão manométrica na saída.

A 1 é a área da seção transversal na entrada.

A 2 é a área da seção transversal na saída.

m ˙ é a taxa de fluxo de massa.

V 1 é a velocidade na entrada.

V 2 é a velocidade na saída.

Passo 2

Vamos calcular a velocidade de saída usando a equação de conservação de massa;

A 1 V 1 = A 2 V 2

Reescrevendo a equação para diâmetros D 1   e   D 2

A 1 V 1 = A 2 V 2

V 2 = A 1 V 1 A 2

V 2 = D 1 2 D 2 2 V 1                         ( 2 )

Vamos usar a seguinte expressão para calcular a pressão manométrica na entrada;

p 1 g = p 1 , a b s - p a t m               ( 3 )

Vamos usar a seguinte expressão para calcular a pressão manométrica na saída;

p 2 g = p 2 , a b s - p a t m               ( 4 )

Vamos calcular a vazão de massa, utilizando a seguinte expressão

m ˙ = ρ A 1 V 1           ( 5 )

Passo 3

Vamos calcular a área da seção transversal na entrada;

A 1 = π 4 D 1 2

A 1 = π 4 ⋅ 0.25 2

A 1 = 0.049   m 2

Vamos calcular a área da seção transversal na saída;

A 2 = π 4 D 1 2

A 2 = π 4 ⋅ 0,08 2

A 2 = 0.005   m 2

Passo 4

Vamos substituir alguns dados numéricos na equação (5);

m ˙ = ρ A 1 V 1

m ˙ = 998 ⋅ 0.049 ⋅ 2.2

m ˙ = 107.58   k g / s

Vamos substituir alguns dados numéricos na equação (4);

p 2 g = p 2 , a b s - p a t m

p 2 g = 120 - 100

p 2 g = 20   k P a

Vamos substituir alguns dados numéricos na equação (3);

p 1 g = p 1 , a b s - p a t m

p 1 g = 350 - 100

p 1 g = 250   k P a

Passo 5

Vamos substituir alguns dados numéricos na equação (2);

V 2 = D 1 2 D 2 2 V 1

V 2 = 0.25 2 0.08 2 ⋅ 2.2

V 2 = 21.48   m / s

Vamos substituir alguns dados numéricos na equação (1);

F p a r a f u s o = p 1 g   A 1 + p 2 g A 2 + m ˙ V 2 + V 1

F p a r a f u s o = 250000 ⋅ 0.049 + 20000 ⋅ 0.005 + 107.58 ( 21.48 + 2.2 )

F p a r a f u s o = 14897.5   N

Resposta

Portanto, a força total a ser resistida pelos parafusos do flange é 14897.5   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

The centrifugal pump of Fig. P3.155 has a fl ow rate Q andexits the impeller at an angle θ2 relative to the blades, asshown. The fl uid enters axially at section 1. Assumingincompressible flow at shaf
A rotating dishwasher arm delivers at 608C to six nozzles,as in Fig. P3.163. The total fl ow rate is 3.0 gal/min. Eachnozzle has a diameter of 16 3 in. If the nozzle fl ows are equaland friction is ne
Revisit the turbine cascade system of Prob. P3.78, andderive a formula for the power P delivered, using theangular momentum theorem of Eq. (3.59).
A centrifugal pump impeller delivers 4000 gal/min ofwater at 208C with a shaft rotation rate of 1750 r/min.Neglect losses. If r1 5 6 in, r2 5 14 in, b1 5 b2 5 1.75 in,Vt1 5 10 ft/s, and Vt2 5 110 ft/s
An airplane is fl ying at 300 mi/h at 4000 m standardaltitude. As is typical, the air velocity relative to the uppersurface of the wing, near its maximum thickness, is 26 percent higher than the plane