Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 6.Problemas - Ex. 56

Indiana Jones precisa subir em um prédio de 10   m de altura. Existe uma mangueira grande cheia com água pressurizada pendurada no alto de prédio. Ele constrói uma plataforma quadrada e monta quatro bocais com 5   c m de diâmetro que apontam para baixo em cada canto. Conectando os ramais da mangueira, um jato d’água com velocidade de 15   m / s pode ser produzido de cada bocal. Jones, a plataforma e os bocais têm uma massa combinada de 150   k g . Determine ( a ) a velocidade mínima do jato d’água necessária para elevar o sistema, ( b ) quanto tempo é preciso para que o sistema se eleve a 10   m quando a velocidade do jato d’água for de 15   m / s e a velocidade da plataforma naquele momento e ( c 0 até onde o momento elevará Jones se ele fechar a água no momento em que a plataforma atingir 10   m acima do solo. Quanto tempo ele tem para pular da plataforma para o teto?

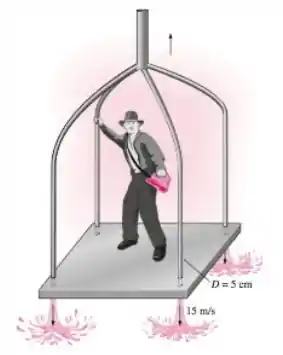
Passo 1

Fala aí galera, bora resolver essa questão de Mecânica dos Fluidos. O caudal mássico total da água através das 4 mangueiras e o peso total da plataforma são dados por:

m ˙ = ρ A V m ˙ = 4 ρ π D 2 4 V m ˙ = 4 1000 k g m 3 π 0,05   m 2 4 15 m s

m ˙ = 118   k g / s

E então parao peso, temos:

W = m g 150   k g 9,81   m / s 2 ) 1   N 1   k g ∙ m s 2 W = 1472   N

Passo 2

Agora, temos que a equação do momento para o escoamento unidimensional constante é dada por:

∑ F → = ∑ s a í d a β m ˙ V → -   ∑ e n t r a d a β m ˙ V →

Então, a velocidade mínima do jato de água necessária para elevar a plataforma é determinada definindo a força líquida que atua na plataforma igual a zero, logo:

- W = m ˙ - V m i n - 0 W = m ˙ V m i n = ρ A V m i n 2 = 4 ρ π D 2 4 V m i n 2

Substituindo: V m i n = 13,7   m / s

Passo 3

Depois, deixamos que a força de reação vertical (assumida para cima) que atua na plataforma seja F R z . Então, a equação do momento na direção vertical vai ser:

F R z - W = m ˙ - V - 0 = m ˙ V F R z = W - m ˙ V F R z = 1472   N - 118 k g s 15 m s F R z = 298   N

O empuxo ascendente que atua na plataforma é igual e oposto a essa força de reação e, portanto, F = 298   N . Então, a aceleração e o tempo de ascensão aumentam 10   m e a velocidade naquele momento se tornam:

a = F m = 298   N 150   k g a = 2   m / s 2

O tempo de ascensão é dado por:

x = 1 2 a t 2 t = 3,2   s

E para velocidade, temos:

V = a t = 2 m s 2 3,2   s V = 6,4   m / s

Passo 4

Por fim, quando a água é cortada a 10   m de altura (onde a velocidade é de 6,4   m / s ), a plataforma desacelera sob a influência da gravidade, e o tempo necessário para pará-la é dado por:

V = V 0 - g t = 0 t = V 0 g = 6,4 m s 9,81 m s 2 t = 0,65   s

E o aumento adicional acima de 10   m se torna:

z = V 0 t - 1 2 g t 2 = 6,4 m s 0,65   s - 1 2 9,81 m s 2 0,65   s 2 z = 2,1   m

Resposta

V m i n = 13,7   m / s

t = 3,2   s

V = 6,4   m / s

t = 0,65   s

z = 2,1   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A curva do tubo da figura abaixo tem D 1 = 27 cm e D 2 = 13 cm. Quando água a 20°C escoa através do tubo com 15142 L/min, p 1 = 194k P a (manométrica). Calcule o torque necessário no ponto B para mant
O rotor de uma bomba centrífuga fornece 15142 L/min de água a 20°C com uma rotação de eixo de 1750 rpm. Despreze as perdas. Se r 1 = 150m m , r 2 = 350m m , b 1 = b 2 = 44m m , V t 1 = 3m / s e V t 2
The centrifugal pump of Fig. P3.155 has a fl ow rate Q andexits the impeller at an angle θ2 relative to the blades, asshown. The fl uid enters axially at section 1. Assumingincompressible flow at shaf
A rotating dishwasher arm delivers at 608C to six nozzles,as in Fig. P3.163. The total fl ow rate is 3.0 gal/min. Eachnozzle has a diameter of 16 3 in. If the nozzle fl ows are equaland friction is ne
Revisit the turbine cascade system of Prob. P3.78, andderive a formula for the power P delivered, using theangular momentum theorem of Eq. (3.59).