Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 155

The centrifugal pump of Fig. P3.155 has a fl ow rate Q and

exits the impeller at an angle θ2 relative to the blades, as

shown. The fl uid enters axially at section 1. Assuming

incompressible flow at shaft angular velocity ω, derive a

formula for the power P required to drive the impeller.

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

Calcule o torque produzido.

T = ρ Q r 2 V t 2 - r 1 V t 1

Aqui, ρ é a densidade, a taxa de fluxo é Q , os raios de entrada e saída são r 1 e r 2 , e as velocidades tangenciais na saída e entrada são V t 2 e V t 1 .

T   = ρ Q r 2 V t 2 - r 1 ( 0 )   = ρ Q r 2 V 12

Passo 2

O diagrama de velocidade para a bomba é o seguinte:

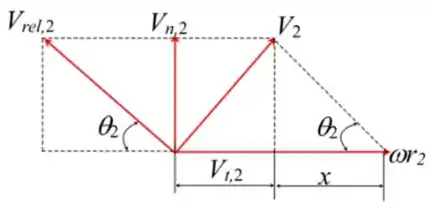
Passo 3

A velocidade de saída absoluta V 2 é obtida adicionando a velocidade de rotação da ponta da lâmina ω r 2 para Escrever a V rel,  2 relação para a velocidade normal na saída.

V n 2 = Q A saida  

Aqui, a velocidade na saída é A saida   . Substitua 2 π r 2 b 2 para A saida   .

V n 2 = Q 2 π r 2 b 2

Aqui, a largura é b 2 .

Passo 4

A velocidade radial na saída é a seguinte:

V r 2 = r 2 ω - V n 2 c o t ⁡ θ 2

Aqui, a velocidade angular é ω .

V t 2 = r 2 ω - Q 2 π r 2 b 2 c o t ⁡ θ 2

Calcule a potência necessária para acionar o impulsor.

P = T ω

Substituindo valores

P = ρ Q 2 V t 2 ω

Substituindo valores

P   = ρ Q r 2 r 2 ω - Q 2 π r 2 b 2 c o t ⁡ θ 2 ω   = ρ Q r 2 ω r 2 ω - Q 2 π r 2 b 2 c o t ⁡ θ 2

Portanto, a potência necessária para acionar o impulsor é

P = ρ Q r 2 ω r 2 ω - Q 2 π r 2 b 2 c o t ⁡ θ 2

Resposta

P = ρ Q r 2 ω r 2 ω - Q 2 π r 2 b 2 c o t ⁡ θ 2

Exercícios de Livros Relacionados

Repita o Problema 6-24 para o caso de theta = 110 ° .
Expresse a equação do momento angular na forma escalar com relação a um eixo especificado de rotação para um volume de controle fixo para escoamento em regime permanente e uniforme.
A água entra em uma bomba centrífuga de forma axialmente à pressão atmosférica, a uma taxa de 0,12m 3 / s e a uma velocidade de 7m / s , e sai na direção normal ao longo da carcaça da bomba, como most
Reconsidere o Problema 6-32. Usando o EES (ou outro software) investigue o efeito da velocidade da placa sobre a força exercida na placa. Faça a velocidade da placa variar de 0 a 30m / s em incremento
Reconsidere o helicóptero do Problema 6-34, exceto que ele flutua no alto de uma montanha de 3000m de altitude na qual a densidade do ar é 0,79k g / m 3 . Observando que as pás do helicóptero descarre