Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 65
Em uma indústria de alimentos, dois fluidos imiscíveis são bombeados através de um tubo de modo que o fluido 1 forme um núcleo de e o fluido 2 forme um espaço anular externo. O tubo tem de diâmetro e comprimento . Deduza e trace a distribuição de velocidade, se a diferença de pressão aplicada, , é 5 MPa.
Passo 1
Tá legal, a primeira coisa que vamos fazer aqui é utilizar a equação 8.11 vista nesse capítulo para o perfil de velocidade, então, temos:
Então, no nosso caso, nós temos que aplicar essa equação para o fluido 1 e para o fluido 2, então, teremos:
O nosso trabalho agora é encontrar as constantes das equações acima, e, como temos 4 constantes, precisamos de 4 condições de contorno. Nós sabemos que na extremidade (parede), em , teremos velocidade do fluido 2 igual a zero. Então, podemos escrever:
Substituindo essa condição na equação para o perfil de velocidade do fluido 2, chegamos em:
Essa será nossa equação 1. Sabemos também que na interface entre os fluidos, eles devem ter a mesma velocidade, dessa forma, temos ocorrendo em , então, substituindo esses valores nos dois perfis de velocidade, temos:
E, igualando as duas equações, temos:
Essa será nossa equação 2.
Passo 2
Agora, nossa terceira condição de contorno será a de velocidade constante com relação ao raio no ponto central do tubo, ou seja em . Isso se deve a simetria do eixo radial. Então podemos escrever:
Então, derivando a expressão de em relação a , temos:
Então, substituindo as condições de contorno para o nosso caso, temos:
Nesse caso, para que o termo restante não tenda a infinito quando , devemos ter . Já achamos a nossa primeira constante. Agora, a nossa última condição de contorno será a de que na interface devemos ter a mesma tensão de cisalhamento entre os fluidos, então, temos:
Já encontramos a expressão para a derivada da velocidade em função de , a expressão para terá o mesmo formato, só que com constantes diferentes. Então, igualando essas duas expressões, temos:
Substituindo o ponto e o valor da constante já encontrada, temos:
Agora, substituindo o valor da constante na nossa equação 1, chegamos em:
E, agora, por fim, substituindo as constantes conhecidas na equação 2, temos:
Passo 3
Então, com todas as constantes determinadas, os perfis de velocidade serão:
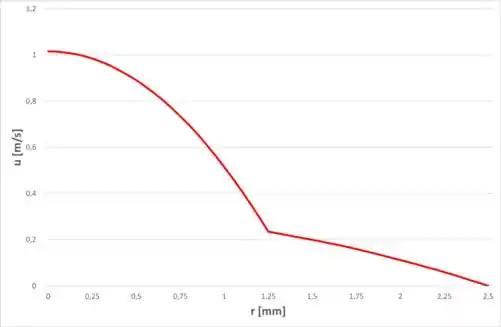
Então, agora podemos traçar o perfil de velocidade, então, colocando essas equações em um gráfico, temos:
