Inicia-se a aplicação de um revestimento plástico em painéis de madeira pela deposição de polímero fundido sobre o painel e o posterior resfriamento da superfície do polímero ao submetê-la a uma corrente de ar a. Como uma primeira aproximação, o calor de reação associado à solidificação do polímero pode ser desprezado e a interface polímero/madeira pode ser considerada adiabática.

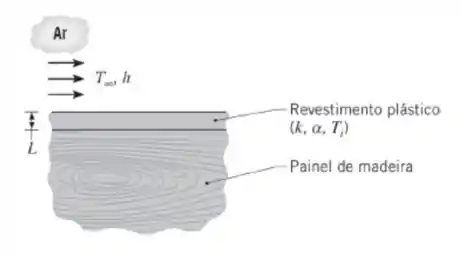
Sendo a espessura do revestimento e ele estando a uma temperatura inicial de , quanto tempo é necessário para a superfície atingie a temperatura segura para o toque de , se o coeficiente de transferência de calor por convecção for ? Qual é o valor correspondente da temperatura da interface? A condutividade térmica e a difusividade térmica do plástico são: e , respectivamente.

Faaalaaa jooveeem!! Bora riscar mais um exercício dessa lista aí?? Vamos juntos!!

Bom, apesar de parecer e de certa forma até ser um bocado longo, não tem segredo nenhum nesse exercício.

Vamos começar como sempre fazemos, encontrando o tio Biot:

Buscando na tabela 5.1 do livro, encontramos o seguinte:

E

Beleza, vamos tentar encontrar então o Fourier, pois é ele que nos dá o tempo que queremos:

Mas nessa fórmula não é possível para nós isolarmos o , pois a gente não sabe o valor de

Então, vamos usar essa outra aqui:

Onde:

E então para isolar vamos precisar saber , e se adotarmos que: , isso só poderá ser possível se, .

Vamos fazer assim então e ver se da certo:

Passando o ln:

Teremos:

Dica gloriosa: lembre-se que é dado em radianos na tabela. Lembre-se então, de passar sua calculadora para radianos na hora de calcular.