Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 43
43. Considere a solução em série, Equação 5.42, para a parede plana com convecção. Calcule as temperaturas θ* no seu plano central (x* = 0) e na sua superfície (x* = 1) para Fo = 0,1 e 1, usando Bi = 0,1; 1 e 10. Considere somente os quatro primeiros autovalores. Com base nesses
resultados, discuta a validade das soluções aproximadas, Equações 5.43 e 5.44.
Passo 1
Escrevendo a equação da solução em série para a parede plana com convecção temos:
Na forma dimensional de dependência, a solução em série para parede plana com convecção pode ser escrita da seguinte maneira:
Em que as equaçãoes para o número de Biot e as constantes são:
Considere que a solução em série tem quatro valores próprios.
Então vamos escrever a equação dos quatro primeiros valores de eigen para a solução em série.
Obtenha os valores de Eigen na tabela “Coeficientes usados na aproximação de um termo para as soluções em série para condução unidimensional transitória” e tabule os quatro primeiros valores de Eigen para diferentes números de Biot.
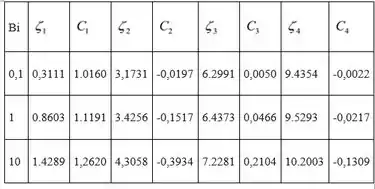
Passo 2
Cálculo de amostra para a temperatura no meio do plano da parede plana com convecção para o número de Fourier e no número de Biot :
Para o plano médio,
Substitua os valores correspondentes da tabela na equação (1).
Cálculo de amostra para a temperatura no meio do plano da parede plana com convecção para o número de Fourier e no número de Biot :
Para o plano médio,
Substitua os valores correspondentes da tabela na equação (1).
Tabule os valores da temperatura média e da superfície da parede do plano com convecção para o número de Fourier .
No número Biot
Tabela 1):Tabule os valores da temperatura média e da superfície da parede do plano com convecção para o número de Fourier .
No número Biot
Tabela 2):
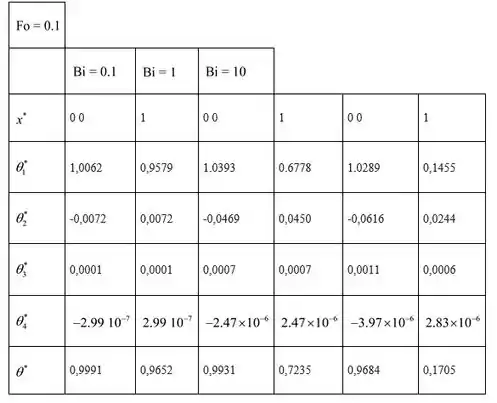
Passo 3
Assim, a partir dos valores calculados acima na tabela (1) e (2), é muito claro que o primeiro valor Eigen é suficiente para calcular a temperatura da parede plana para o número de Fourier igual a 1. Mas, no caso do número de Fourier de 0.1, a temperatura da parede plana é decidida pelos três primeiros valores de Eigen.
Na literatura, as soluções aproximadas são válidas para o número de Fourier maior que 0,2. Para verificar a validade, repita os cálculos acima para o número de Fourier igual a 0,2.
Calcular a temperatura da parede plana com convecção tem um número de Fourier,
E número Biot
Para o plano médio,
Tabular os valores das temperaturas da parede do plano médio com convecção tem um número de Fourier ,.
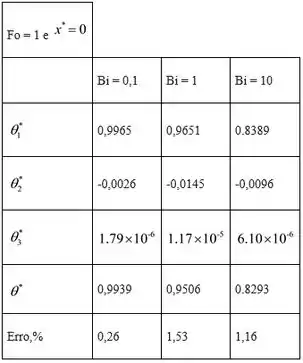
Assim, a solução aproximada para a série terá apenas o primeiro termo de valor próprio. Com base no cálculo de erro na tabela acima, pode-se afirmar que o efeito do segundo termo e outros termos são negligenciáveis para o número Biot 0,1, enquanto o efeito é em torno de no máximo 1,5% para o número Biot maior que 1.
Resposta
Discussão em texto.