Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 76
Trabalhe o Problema 5.47 para o caso de uma esfera de raio ro.
Passo 1
Primeiro, vamo resolver a primeira parte do item (a).
Pra isso, se a gente supor tempos muito longos () podemos modelar a temperatura adimensional na superfície () a partir da equação:
Podemos também modelar a temperatura adimensional do eixo central a partir da equação:
Sendo e coeficientes que podem ser calculados a partir da Tabela 5.1, o adimensional Número de Fourier.
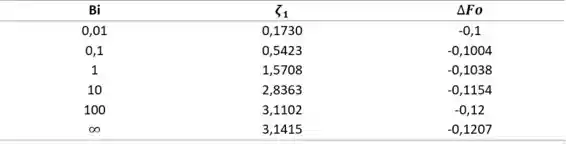
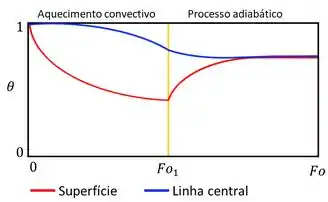
Vamo então traçar um esboço do gráfico da variação de temperatura adimensional da esfera, tanto para a superfície quanto para o eixo central da esfera:
Vamo analisar esse gráfico juntos.
Em primeiro lugar, ao ser colocado um isolante no tempo adimensional , o processo passa de um aquecimento convectivo para um processo adiabático.
Não se avexe, não! A gente vai analisar os dois processos separadamente e entender o que ocorre.
- Aquecimento Convectivo
- Processo Adiabático
Devemos lembrar que a temperatura adimensional da superfície é igual a /, o que significa que quanto maior o tempo adimensional ( ), maior a temperatura da superfície (. Isso quer dizer que mais a temperatura da superfície vai se aproximar da temperatura do fluido (), diminuindo o gradiente de temperatura e a taxa de transferência de calor, e a temperatura adimensional da superfície vai decaindo exponencialmente.
O mesmo ocorre com a temperatura adimensional do eixo central ( , com a única diferença de que, como e a resistência à transferência de calor por condução da superfície até o centro é significativa, a temperatura do centro aumenta a uma taxa menor que a temperatura da superfície, e portanto se mantém bem menor que .
Depois de colocar um isolante na esfera no tempo , não há mais transferência de calor do fluido para a superfície da esfera. Começa, então, uma transferência de calor por condução da superfície para o eixo central.
Sendo assim, a temperatura diminui e, portanto, se distancia mais de , aumentando . Por outro lado, continua aumentando, se aproximando de , diminuindo .
O processo continua até que se iguale a (), e a esfera entre em equilíbrio térmico.
Passo 2
Vamo resolver agora a segunda parte do item (a).
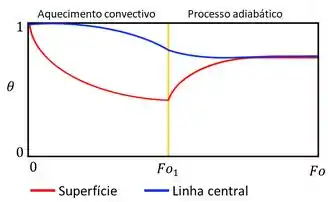
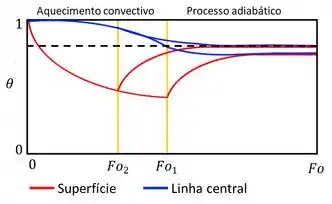
Vamos olhar pra esse gráfico:
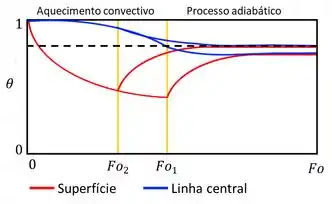
Os processos que tão acontecendo nesse gráfico são iguais àqueles que te mostrei no Passo 1. A diferença aqui é que o isolante seria colocado num tempo adimensional , no qual o novo estado estacionário estaria na altura da linha tracejada que também marca a temperatura do centro no tempo .
Com o processo seguindo de maneira igual ao do passo anterior, temos que é um tempo adimensional que deve estar posicionado antes de , pois seu estado estacionário (equilíbrio térmico) ocorre antes daquele obtido quando é o ponto onde se coloca o isolante.
Logo, .
Passo 3
Vamos resolver o item (b) agora.
Devemos achar uma expressão para considerando as condições dos Passos 1 e 2 e que que .
Vamos demonstrar uma relação entre a temperatura adimensional em e a energia transferida em .
Primeiramente, vamos relembrar a expressão para a razão entre quantidade de energia transferida e a máxima energia possível de ser transferida:
Ou seja, na prática, essa razão pode ser entendida, em termos de unidades, como uma temperatura adimensional.
Vamos analisar então o gráfico do Passo 2. Ele diz pra gente que a temperatura do eixo central no tempo é igual à temperatura estacionária a partir do tempo . Isso significa que, a partir de , a energia transferida continua a mesma (já que o processo é adiabático, sem troca de calor) e, por isso, , sendo a temperatura adimensional que vimos na expressão acima.
Dessa maneira, podemos definir a seguinte expressão para uma relação entre a temperatura adimensional em e a energia transferida em :
A gente tem que lembrar também que, para uma esfera, podemos calcular a energia transferida a partir da expressão:
Portanto, voltando à nossa expressão deduzida:
Vamos lembrar, ainda, que e
Devemos usar a propriedade de exponenciais:
Vamos isolar :
Vamos aplicar em ambos os lados da equação:
Sendo assim, nossa expressão para se torna:
Se utilizarmos as condições dadas na questão, fazendo , teremos que, pela Tabela 5.1, .
Logo, o valor de pode ser calculado como:
Passo 4
Pra finalizar, vamos resolver o item (c) agora.
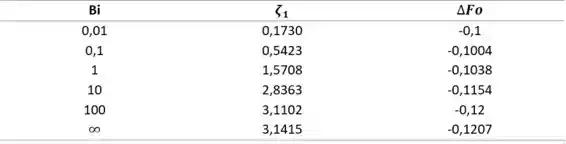
Devemos calcular o valor de para diversos valores de .
O procedimento é análogo ao que a gente fez no passo anterior. Vamos à Tabela 5.1 com o valor de , e buscamos o valor de . Depois, a gente vai calcular o valor de pela equação.
Fazendo isso para todos os valores de Biot pedidos pelo enunciado, a gente pode montar a seguinte tabelinha:
UFA! Demorou, mas a gente matou a questão!
Resposta
(a) Os esboços gráficos para as condições dadas são:
(b) Deduzimos a seguinte expressão: e, para Bi = 1, .
(c) 