Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo Exercícios Selecionados.- - Ex. 16

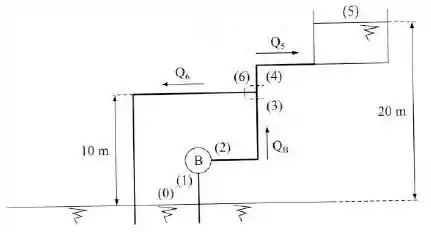
Na instalação da figura, a bomba envia 5   L / s de água ( γ = 10 4   N / m 3 ) para o reservatório superior e uma parte da vazão retorna para o tanque inferior. Dados: P 6 = 100   k P a ; H p 6,0 = 25   m ; H p 0,1 = 10   m ; H p 2,3 = 5   m ; H p 3,4 , 6 = 0 ; potência fornecida ao fluido pela bomba: N = 12   k W ; área da seção de todas as tubulações: A = 10   c m 2 . Determinar:

  1. A vazão que retorna ao tanque inferior ( Q 6 ) ;
  2. A carga manométrica da bomba;
  3. A perda de carga de ( 4 ) a ( 5 ) ;
  4. A potência dissipada em toda a instalação.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Para calcular a vazão que retorna ao tanque Q 6 , utilizaremos a equação de Bernoulli para o trecho 6 - 1 , supondo o tanque 0 à pressão atmosférica P 0 = 0 e de grandes dimensões v 0 = 0 :

H 6 = H 0 + H p 6,0

P 6 γ + v 6 2 2 g + z 6 = P 0 γ + v 0 2 2 g + z 0 + H p 6,0

Substituindo os valores, temos que:

10 5 10 4 + v 6 2 20 + 10 = 25

v 6 = 10   m / s

Passo 2

A vazão será:

Q 6 = v 6 ⋅ A 6

Q 6 = 10 ⋅ 10 ⋅ 10 - 4

Q 6 = 10   m 3 / s

Ou:

Q 6 = 10   L / s

Passo 3

Para calcular a carga manométrica da bomba, devido a conservação de massa do fluido incompressível, temos que:

Q 4 + Q 6 = Q 3

Q 3 = 10 + 5

Q 3 = 15   L / s

Também pela conservação de massa, sabemos que a vazão volumétrica do ponto 3 é igual a vazão volumétrica do ponto 1 . Além disso conhecemos a relação para a potência fornecida pela bomba, onde H B é a carga manométrica:

N B = γ Q 1 H B

12000 = 10 4 ⋅ 15 ⋅ 10 - 3 ⋅ H B

H B = 80   m

Passo 4

Para entender o que acontece no trecho 4 - ( 5 ) , vamos estudar o trecho 0 - ( 3 ) segundo Bernoulli:

80 = P 3 10 4 + 15 2 20 + 10 + 10 + 5

P 3 = 437,5   k P a

Conhecendo as quantidades relacionadas ao ponto ( 3 ) , podemos estudar o fluxo de energia na bifurcação, sabendo que:

E 3 = E 4 + E 6 + H p 3,4 , 6

γ Q 3 P 3 γ + v 3 2 2 g + z 3 = γ Q 4 P 4 γ + v 4 2 2 g + z 4 + γ Q 6 P 6 γ + v 6 2 2 g + z 6 + H p 3,4 , 6

Substituindo os valores conhecidos temos que:

10 4 15 ⋅ 10 - 3 437,5 ⋅ 10 3 10 4 + 15 2 2 0 + 10 = 10 4 5 ⋅ 10 - 3 P 4 10 4 + 5 2 10 + 10 + 10 4 10 ⋅ 10 - 3 10 5 10 4 + 10 2 2 0 + 10

P 4 = 1337,5   k P a

Por fim, estudemos o trecho 4 - 5 , também segundo Bernoulli:

P 4 γ + v 4 2 2 g + z 4 = P 5 γ + v 5 2 2 g + z 5 + H p 4,5

Substituindo pelos valores conhecidos, temos que:

1337,5 ⋅ 10 3 10 4 + 5 2 10 + 10 = 20 + H p 4,5

H p 4,5 = 125   m

Passo 5

A potência total dissipada é a somatória de todas as potências dissipadas em cada trecho:

N = ∑ N i

N = N 0,1 + N 2,3 + N 6,0 + N 4,5

Desenvolvendo, temos que:

N = γ A v 1 H p 0,1 + v 3 H p 2,3 + v 6 H p 6,0 + v 4 H p 4,5

Substituindo os valores, temos que:

N = 10 4 ⋅ 10 - 3 15 ⋅ 10 + 15 ⋅ 5 + 5 ⋅ 25 + 5 ⋅ 125

N = 14   k W

Resposta

a )   Q 6 = 10   L / s

b )   H B = 80   m

c )   H p 4,5 = 125   m

d )   N = 14   k W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em uma usina hidrelétrica, a água entra nos bocais da turbina a 700k P a absoluta com baixa velocidade. Se as saídas do bocal são expostas à pressão atmosférica de 100k P a , determine a velocidade má
Reconsidere o problema 5-61. Determine a vazão da água e a diferença de pressão através da bomba se a perda de carga do sistema de tubulação for de 5 m .
Uma sonda estática de Pitot conectada a um manômetro de água é usada para medir a velocidade do ar. Se a deflexão (a distância vertical entre os níveis de fluido nos dois braços) for de 7,3c m , deter
A água subterrânea deve ser bombeada por uma bomba submersa de 3k W e eficiência de 70 % para uma piscina cuja superfície livre está 30m acima do nível da água subterrânea. O diâmetro do tubo é de 7 c
Como a localização da linha piezométrica é determinada no escoamento de canal aberto? Como ela é determinada na saída de um cano que descarga na atmosfera?