Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo Exercícios Selecionados.- - Ex. 24

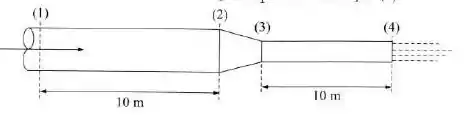
No trecho 1 - ( 2 ) do conduto da figura, o escoamento do fluido ( γ = 8000   N / m 3 ) é laminar, a vazão é 10   L / s , o diâmetro é 8   c m e o R e = 1000 . No trecho 3 - 4 o diâmetro é 6   c m . O coeficiente da perda de carga da singularidade 2 - 3 é 1 , referente à maior velocidade. Qual a pressão na seção 1 ?

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Para calcular a velocidade de escoamento de ar, vamos primeiramente, calcular o diâmetro hidráulico de escoamento para, em seguida olhar para a equação de perda de carga. O diâmetro hidráulico:

D h , a r = A σ

Desenvolvendo, temos que:

D h , a r = π D 3 2 2 - π D 2 2 2 2 π D 3 2 + 2 π D 2 2

Podemos simplificar:

D h , a r = D 3 - D 2 4

Substituindo os valores, temos que:

D h , a r = 740 - 70 4

D h , a r = 0,167   m

Conhecido o diâmetro hidráulico do escoamento de ar, utilizemos a equação de perda de carga distribuída para conhecer a velocidade de escoamento:

H p , a r = f L D h , a r ⋅ v a r 2 2 g

3 ⋅ 4 = 0,01 4 0,668 ⋅ v a r 2 2 g

v a r = 63,4   m / s

Passo 2

Para calcular a velocidade de escoamento de combustível, vamos utilizar a relação de fluxo mássico dado, para o ar:

A a r = π D 3 2 2 - π D 2 2 2

A a r = π 0,74 2 2 - π 0,07 2 2

A a r = 0,426   m 2

Para o combustível teremos:

A c o m b = π D 1 2 2

A c o m b = π 0 , 065 2 2

A c o m b = 0 , 003   m 2

Agora, analisemos as relações de fluxo mássico exigidas:

m ˙ a r m ˙ c o m b = 10 1

ρ a r Q a r ρ c o m b Q c o m b = 10 1

ρ a r A a r v a r ρ c o m b A c o m b v c o m b = 10 1

Substituindo os valores, temos que:

2 ⋅ 0,426 ⋅ 63,4 800 ⋅ 0,003 ⋅ v c o m b = 10 1

v c o m b = 2 m / s

Passo 3

Para estudar a perda por carga distribuída no escoamento de combustível, vamos avaliar o escoamento segundo o número de Reynolds.

R e = v D v

R e = 2 ⋅ 0,065 10 - 4

R e = 1300

Portanto o escoamento é laminar, logo:

f = 64 R e

f = 0,049

Conhecido o coeficiente de perda por carga generalizada, temos que:

H p , c o m b = f ⋅ L D h , c o m b ⋅ v c o m b 2 2 g

H p , c o m b = 0,049 ⋅ 4 0,065 ⋅ 2 2 2 0

H p , c o m b = 0,6   m

Resposta

a )   v a r = 63,4   m / s

b )   v c o m b = 2 m / s

c )   H p , c o m b = 0,6   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Repita p Problema 8 - 37 para o escoamento turbulento em tubos suaves para os quais o fator de atrito é dado por f = 0,184 R e - 2 . Qual seria a sua resposta para um escoamento totalmente turbulento
Amônia líquida a - 20 ° C escoa através de uma seção de 30m de comprimento de um tubo de cobre com 5m m de deâmetro a uma taxa de 0,15 k g / s . Determine a queda de pressão, a perda de carga e a potê
Em um sistema de aquecimento de ar, o ar aquecido a 40 ° C e 105k P a absoluta é distribuído através de um duto retangular de 0,2m× 0,3m feito de aço comercial a uma taxa de 0,5m ³ / s ³ . Determine a
Óleo com ρ = 876k g / m ³ ³ e μ = 0,24k g / m . s escoa através de um tubo com 1,5c m de diâmetro que descarrega na atmosfera a 88k P a . A medida da pressão absoluta 15m antes da saída é 135k P a . D
Glicerina a 40 ° C com ρ = 1,252k g / m ³ ³ e μ = 0,27k g / m . s escoa através de um tubo com 2c m de diâmetro de 25m de comprimento que descarrega na atmosfera a 100k P a . A vazão através do tubo é