Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 4.Exercício - Ex. 14

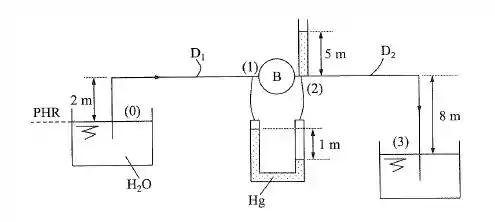
Na instalação da figura, a carga total na seção 2 é 12   m . Nessa seção, existe um piezômetro que indica 5   m . Dados: γ H 2 O = 10 4   N / m 3 ; γ H g = 1,36 × 10 5   N / m 3 ; h = 1   m ; D 1 = 6   c m ; D 2 = 5   c m ; η B = 0,8 . Determinar:

  1. A vazão;
  2. A pressão em 1 ;
  3. A perda de carga ao longo de toda a tubulação;
  4. A potência que o fluido recebe da bomba.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Para determinar a vazão, temos que encontrar a velocidade do escoamento em algum ponto. Sabemos que:

H 2 = 12   m

Logo:

12 = z 2 + v 2 2 2 g + P 2 γ

Resolvendo, temos que:

v 2 = 2 g 12 - P 2 γ - z 2

Substituindo as variáveis, temos que:

v 2 = 2 ⋅ 10 12 - 5 - 2

v 2 = 10   m / s

Passo 2

Dada a velocidade, a vazão é obtida por:

Q = v 2 ⋅ π 4 D 2 2

Q = 10 ⋅ π 4 ⋅ 0,05 2

Resolvendo, temos que:

Q = 0,0196   m 3 / s

Q = 19,6   L / s

Passo 3

A pressão no ponto 1 é obtida pela seguinte expressão da equação manométrica:

P 1 + γ H g h - γ h = P 2

P 1 = P 2 + h γ - γ H g

Substituindo os valores, temos que:

P 1 = 5 ⋅ 10 4 + 1 10 4 - 1,36 ⋅ 10 5

P 1 = - 76000   P a

Passo 4

A velocidade no ponto 1 é dada a partir da equação da continuidade:

v 1 A 1 = v 2 A 2

v 1 = v 2 D 2 2 D 1 2

Substituindo os valores, temos que:

v 1 = 10 5 6 2

v 1 = 6,9   m / s

Podemos então encontrar a carga na bomba:

H B = v 2 2 - v 1 2 2 g + P 2 - P 1 γ

Substituindo os valores temos que:

H B = 10 2 - 6,9 2 20 + 5 - - 76000 10 4

H B = 15,2   m

Passo 5

Logo, a perda de carga total é calculada por:

H 0 + H B = H 3 + H p 0,3

H p 0,3 = z 0 - z 3 + H B

Substituindo os valores, temos que:

H p 0,3 = 8 - 2 + 15,2

H p 0,3 = 21,2   m

A potência que a bomba fornece ao fluido é dada por:

N = γ Q H B

N = 10 4 ⋅ 0,0196 ⋅ 15,2

N = 3   k W

Resposta

a )   Q = 19,6   L / s

b ) P 1 = - 76000   P a

c )   H p 0,3 = 21,2   m

d )   N = 3   k W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O ventilador do banheiro de um prédio tem uma vazão de volume de 30 L/s e funciona continuamente. Se a densidade do ar interno é de 1,20 kg/m³, determine a massa do ar que é expelida ou que sai em um
A energia elétrica deve ser gerada pela instalação de uma turbina gerador-hidráulica em um local 70 m abaixo da superfície livre de um grande reservatório de água que pode fornecer água a uma vazão de
Um computador pessoal deve ser resfriado por um ventilador cuja vazão é de 0,34 m³/min. Determine a vazão de massa do ar através do ventilador a uma elevação de 3.400 m, onde a densidade do ar é de 0,
Ar entra em um bocal de forma constante a 2,21 kg/m³ e 30 m/s e sai a 0,762 kg/m³ e 180 m/s. Se a área de entrada do bocal é de 80 cm², determine (a) a vazão em massa através do bocal e (b) a área de
Em determinado local, o vento sopra em regime permanente a 12 m/s. Determine a energia mecânica do ar por unidade de massa e o potencial de geração de potência de uma turbina de vento com lâminas de 5