Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo Exercícios Selecionados.- - Ex. 9

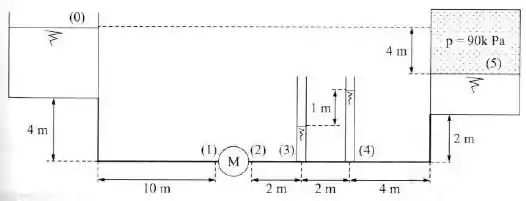
Na instalação da figura são dados: Q = 4   L / s ; área da seção das tubulações A = 20   c m 2 ; potência da máquina N M = 0,19   k W ; perda de carga distribuída é diretamente proporcional ao comprimento da tubulação; as perdas de carga singulares são desprezíveis; o fluido é óleo de peso específico 8000   N / m 3 . Determinar:

  1. O sentido do escoamento;
  2. A perda de carga na instalação;
  3. O tipo de máquina;
  4. A diferença de pressão entre a entrada e a saída da máquina;
  5. O rendimento da máquina.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O item “a” nos pede o sentido do escoamento. Se observarmos bem, o sistema tem dois tanques e o primeiro no ponto 0 está acima do segundo no ponto 5 .

Portanto, pela ação da gravidade o sentido do escoamento será da esquerda para a direita. De 0 → 5 .

Passo 2

O item “b” nos pede a perda de carga na instalação. Vamos aplicar então a equação de perda de carga saindo do ponto 0 até chegar no ponto 5 :

H p 1 , 2 = H 0 - H 5

Desenvolvendo, temos que:

H p 1,2 = α 0 v 0 2 - α 0 v 0 2 2 g + P 0 - P 5 γ + z 0 - z 5

H p 1,2 = h f 1,2

Vamos adotar as hipóteses de que a pressão no ponto 0 é atmosférica, portanto, P 0 = 0 . Pela equação da continuidade sabemos que as velocidades são iguais. Portanto:

h f 1,2 = - P 5 γ + z 0 - z 5

Substituindo os valores, temos que:

h f 1,2 = - 90000 8000 + - 4

h f 1,2 = - 15,25   m

Passo 3

O item “c” nos pede o tipo de máquina.

Existem dois tipos de máquinas para o nosso sistema. A bomba e a turbina. A bomba fornece energia ao sistema gerando uma perda de carga positiva, enquanto a turbina recebe energia do sistema gerando uma perda de carga negativa.

Dos passos anteriores, sabemos que pela ação da gravidade o sistema gera energia para a máquina e sua perda de carga é negativa, logo, podemos dizer que se trata de uma turbina.

Passo 4

O item “d” nos pede a diferença de pressão na saída da máquina, ou seja, entre os pontos 3 e 4 .

Podemos fazer uma análise manométrica a partir das alturas das colunas do fluido. Temos que:

∆ P = ρ g z 4 - z 3

Ou:

∆ P = γ ∆ z

Substituindo os valores, temos que:

∆ P = 8000 ⋅ 1

∆ P = 8000   P a

Passo 5

O item “e” nos pede o rendimento da máquina. O rendimento de uma turbina é dado por:

η = N γ Q H

Substituindo os valores, temos que:

η = 0,19 ⋅ 10 3 8000 ⋅ 4 ⋅ 10 - 3 ⋅ 15,25

Resolvendo, encontramos:

η = 38,93   %

Resposta

a )   O   s e n t i d o   d o   e s c o a m e n t o   é   d a   e s q u e r d a   p a r a   a   d i r e i t a . 0 → 5 .  

b )   h f 1,2 = - 15,25   m

c )   T u r b i n a

d )   ∆ P = 8000   P a

e )   η = 38,93   %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma pessoa afirma que no escoamento turbulento completamente desenvolvido em um tubo, a tensão de cisalhamento está no máximo na superfície do tubo. Você concorda com isso? Explique.
Como a tensão de cisalhamento da parede τ w varia ao longo da direção de escoamento na região completamente desenvolvida do (a) escoamento laminar e (b) escoamento turbulento?
Considere o escoamento laminar completamente desenvolvido em um tubo circular. Se o diâmetro do tubo for reduzido pela metade enquanto a vazão e o comprimento do tubo forem mantidos constantes, a perd
Como o fator de atrito do escoamento em um tubo está relacionado à perda de pressão? Como a perda de pressão está relacionada ao requisito de potência de bombeamento para determinada vazão em massa?
Como a perda de carga está relacionada à perda de pressão? Para determinado fluido, explique como você converteria a perda de carga em perda de pressão.