Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 77
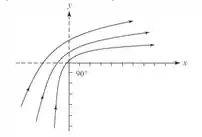
Investigue a função corrente em coordenadas polares . Trace um gráfico das linhas de corrente em todos os quadrantes, exceto o inferior direito, e interprete.
Passo 1
Bora pra mais uma!
Vamos manipular a equação:
Agora, vamos plotar as linhas de corrente, para isso deveremos “chutar” valores de e plotar um gráfico r versus:
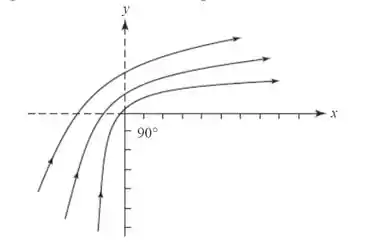
Resposta
As linhas de corrente representam um fluxo invíscido em uma volta de 90.
Exercícios de Livros Relacionados
Um tornado é simulado por uma fonte m =– 1.000m ² / s ² mais um vórtice K = + 1 . 600 m 2 s . Encontre o ângulo entre qualquer linha de corrente e uma linha radial e mostre que ele é independente tant
Para a oval de Rankine na Figura 8.37, se o fluido é água a 20ºC e a pressão bem a jusante ao longo da linha de centro do corpo é de 115 kPa, determine a velocidade da corrente livre U ∞ para que ocor
Modifique a oval de Rankine na Figura 8.37, mantendo a velocidade da corrente e o comprimento do corpo e deixando a espessura como incógnita (não 1 m). O fluido é água a 30 ºC e a pressão bem a jusant
Considere o escoamento não viscoso de estagnação, ψ =K x y (ver a Figura 8.19b) superposto a uma fonte de intensidade m na origem. Trace as linhas de corrente resultantes no semiplano superior, usando
Um escoamento incompressível bidimensional é definido por u = K y x 2 + y 2 v = K x x 2 + y 2 Em que K = constante. Esse escoamento é irrotacional? Em caso afirmativo, encontre seu potencial de veloci