Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 68
Investigue o potencial complexo e interprete o padrão de escoamento.
Passo 1
E aí, tudo bem? Bora matar essa questão!
Basicamente vamos ter a oval mais simples de Rankine que é descrita pela equação , vamos fazer o desenho da nossa figura!
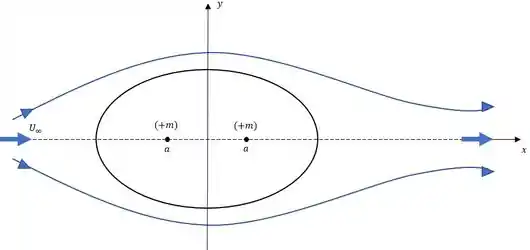
Como encontramos na página do livro texto o escoamento é sobre uma figura oval padrão de Rankine!
Isso é tudo pessoal, conseguimos mais uma! \o/
Resposta
Como encontramos na página do livro texto o escoamento é sobre uma figura oval padrão de Rankine!
Baseada nas equações e !
Desenho vide passo a passo
Exercícios de Livros Relacionados
Transforme a posição x → =( 4 ,3 , -4 ) de coordenadas cartesianas ( x ,y ,z ) em coordenadas cilíndricas ( r ,θ ,z ) , incluindo as unidades. Os valores de x → estão em unidades de metros.
Deixe o vetor G → ser dado por G → = 2 x z i → - 1 2 x 2 j → + z 2 k → . Calcule o divergente de G → , e simplifique o máximo possível. Existe algo de especial no seu resultado?
Quantas incógnitas há para um campo de escoamento tridimensional, em regime não permanente, incompressível, no qual as variações de temperatura são insignificantes? Liste as equações necessárias para
A regra do produto pode ser aplicada ao divergente do escalar f vezes o vetor G → como: ∇ → . f G → = G → . ∇ → f + f ∇ → . G → . Expanda ambos os lados desta equação em coordenadas cartesianas e veri
O produto exterior de dois vetores é um tensor de segunda ordem com nove componentes. Em coordenadas cartesianas, ele é:A regra do produto aplicada à divergência do produto aplicada ao divergente de d