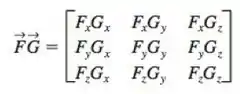Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 11

O produto exterior de dois vetores é um tensor de segunda ordem com nove componentes. Em coordenadas cartesianas, ele é:

A regra do produto aplicada à divergência do produto aplicada ao divergente de dois vetores

dois vetores F → e G → pode ser escrito como ∇ → . F → G → = G → ( ∇ →   .     F → ) + ( F   →   .     ∇ → ) G → . Expanda ambos os lados desta equação em coordenadas cartesianas e verifique se está correta.

Passo 1

Faaaaaala galerinhaa !!

Vamos para mais umaa??

Podemos escrever os vetores como:

G → = G x i + G y j + G z k

F → = F x i + F y j + F z k

∇ → = ∂ ∂ x i + ∂ ∂ y j + ∂ ∂ z k

Portanto o divergente em coordenadas cartesianas serão:

∇ →   .   F → G → = ∂ ∂ x i + ∂ ∂ y j + ∂ ∂ z k . F x G x F x G y F x G z F y G x F y G y F y G z F z G x F z G y F z G z

A primeira coluna da matriz representa a direção i , a segunda a j e a terceira a k !

Portanto:

= ∂ ∂ x F x G x + ∂ ∂ y F y G x + ∂ ∂ z F z G x i + ∂ ∂ x F x G y + ∂ ∂ y F y G y + ∂ ∂ z F z G y j + ∂ ∂ x F x G z + ∂ ∂ y F y G z + ∂ ∂ z F z G z k

Se lembram da Regra do Produto?

“Derivada da primeira vezes a segunda mais a derivada da segunda vezes a primeira!”

Vamos aplicar?

∇ →   .   F → G → = F x ∂ G x ∂ x + G x ∂ F x ∂ x + F y ∂ G x ∂ y + G x ∂ F y ∂ x + F z ∂ G x ∂ z + G x ∂ F z ∂ x i + F x ∂ G y ∂ x + G y ∂ F x ∂ x + F y ∂ G y ∂ y + G y ∂ F y ∂ x + F z ∂ G y ∂ z + G y ∂ F z ∂ x j + F x ∂ G z ∂ x + G z ∂ F x ∂ x + F y ∂ G z ∂ y + G z ∂ F y ∂ x + F z ∂ G z ∂ z + G z ∂ F z ∂ x k

Para ficar mais apresentável nós vamos os termos do vetor G → :

∇ →   .   F → G → = F x ∂ ∂ x + F y ∂ ∂ y + F z ∂ ∂ z G x + G x ∂ F x ∂ x + ∂ F y ∂ x + ∂ F z ∂ x i + F x ∂ ∂ x + F y ∂ ∂ y + F z ∂ ∂ z G y + G y ∂ F x ∂ x + ∂ F y ∂ x + ∂ F z ∂ x j + F x ∂ ∂ x + F y ∂ ∂ y + F z ∂ ∂ z G z + G z ∂ F x ∂ x + ∂ F y ∂ x + ∂ F z ∂ x k

Podemos reescrever alguns termos, não é?

F x ∂ ∂ x + F y ∂ ∂ y + F z ∂ ∂ z = F →   .   ∇ →

∂ F x ∂ x + ∂ F y ∂ x + ∂ F z ∂ x = ∇ →   .   F →

Reparem que a ordem faz toda diferença, não é?

Vamos substituir?

∇ →   .   F → G → = F →   .   ∇ → G x + G x ∇ →   .   F → i + F →   .   ∇ → G y + G y ∇ →   .   F → j + F →   .   ∇ → G z + G z ∇ →   .   F → k

Agora vamos abrir cada termo com relação a direção:

∇ →   .   F → G → = F →   .   ∇ → G x i + G x ∇ →   .   F → i + F →   .   ∇ → G y j + G y ∇ →   .   F → j + F →   .   ∇ → G z k + G z ∇ →   .   F → k

E agora vamos isolar F →   .   ∇ → e ∇ →   .   F → :

∇ →   .   F → G → = F →   .   ∇ → G x i + G y j + G z k + G x i + G y j + G z k ∇ →   .   F →

Olha quem apareceu no meio da confusão, o vetor G → :

∇ →   .   F → G → = F →   .   ∇ → G → + G → ∇ →   .   F →

E the end!!

Comprovamos o que queríamos !

Resposta

∇ →   .   F → G → = F →   .   ∇ → G → + G → ∇ →   .   F →

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Consider potential fl ow of a uniform stream in the x direction plus two equal sources, one at (x, y) 5 (0, 1a) and theother at (x, y) 5 (0, 2a). Sketch your ideas of the bodycontours that would arise
Starting at the stagnation point in Fig. 8.6, the fluid acceleration along the half-body surface rises to a maximumand eventually drops off to zero far downstream. (a) Doesthis maximum occur at the po
A proposed harmonic function F(x, y, z) is given byF 5 2x2 1 y3 2 4xz 1 f(y)(a) If possible, fi nd a function f (y) for which the laplacianof F is zero. If you do indeed solve part (a), can your final
A 22-cm-diameter solid aluminum sphere (SG 5 2.7) is accelerating at 12 m/s2 in water at 208C. (a) According to potential theory, what is the hydrodynamic mass of the sphere?(b) Estimate the force bei
For the velocity distribution u 5 2By, υ 5 1Bx, w 5 0,evaluate the circulation Γ about the rectangular closedcurve defined by (x, y) 5 (1,1), (3,1), (3,2), and (1,2). Interpret your result, especially