12 - Uma janela dupla possui duas placas de vidro, com de espessura cada uma, que confinam uma camada de ar com de espessura. A janela separa o ar da sala a do ar do ambiente externo a . O coeficiente convectivo associado à superfície interna (lado da sala) é de .

(a) Se o coeficiente convectivo associado ao ar externo (ambiente) é de , qual é a perda de calor através de uma janela que possua de altura por de largura? Despreze a radiação e suponha que o ar entre as placas de vidro encontra-se estagnado.

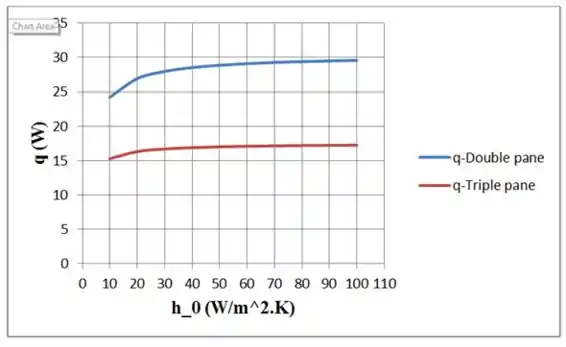
(b) Calcule e represente graficamente o efeito de na perda de calor para . Repita os cálculos para uma janela tripla, na qual a terceira placa de vidro e a segunda camada de ar possuem as mesmas características das existentes na janela dupla.

Antes de começar, precisamos calcular a temperatura de filme. Use a seguinte fórmula:

Aqui,  é a temperatura do ar na superfície interna do vidro e  é a temperatura do ar na superfície externa do vidro.

Por interpolação entre e , obtemos que a condutividade térmica do ar para a temperatura de é:

Para a temperatura de temos que a condutividade térmica do vidro é:

Precisamos encontrar a área do painel duplo.

Aqui,  é o comprimento da janela e  é a largura da janela.

Para acharmos a perda de calor, precisamos encontrar a resistência total.

Por isso, vamos calcular a resistência total da janela de painel duplo. Voltando ao passo temos o desenho do circuito térmico, logo vamos representá-lo abaixo:

Aqui, é a espessura do vidro, é a espessura a camada de ar,  é a área da janela de painel duplo,  é a convecção associada à superfície interna,  é a condutividade térmica do vidro,  é a condutividade térmica do ar e  é o coeficiente de convecção associado ao ar ambiente externo.

Substituindo pelos valores conhecidos, temos:

Agora podemos calcular a perda de calor através de uma janela de painel duplo, com a seguinte equação:

Aqui,  é a temperatura ambiente da condição da superfície interna,  é a temperatura ambiente da condição da superfície externa e  é a resistência total da janela do painel duplo.

Portanto, a perda de calor através de uma janela de painel duplo é .

b)

Escreva a expressão para a perda de calor em uma janela de painel duplo.

Substituindo pelos valores fornecidos, temos a relação que é pedida.

O diagrama do circuito térmico para a janela de painel triplo é representado.

Agora, vamos repetir os processos anteriores, porém para uma janela de painel triplo.

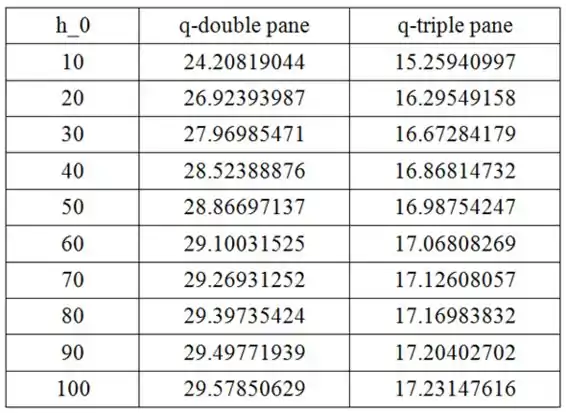
Use as equações e e determine a perda de calor através da janela de painel duplo e triplo, variando o valor de  de  até .

Liste os valores obtidos em uma tabela da seguinte maneira:

Traçar o efeito de  na perda de calor para essa variação: