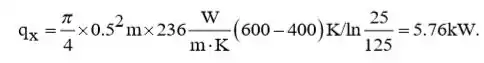Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 39
O diagrama mostra uma seção cônica fabricada em puro alumínio. Ela possui uma seção transversal circular com diâmetro , com . A menor extremidade está localizada em e a extremidade maior em . As temperaturas nas extremidades são e , enquanto a superfície lateral é isolada termicamente.
(a) Deduza uma expressão literal para a distribuição de temperaturas T(x), supondo condições unidimensionais. Esboce a distribuição de temperaturas.
(b) Calcule a taxa de transferência de calor .
Passo 1
Beleza galerinha, vamos lá! (a) Com base nas hipóteses, e seguindo a mesma metodologia do Exemplo 3.4, qx é uma constante independente de x. Assim sendo,
Separação de variáveis e identificação de limites,
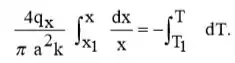
Integração e solução para T(x) e depois para T2,
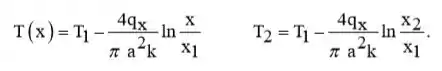
Resolvendo para qx e depois substituindo dá os resultados,
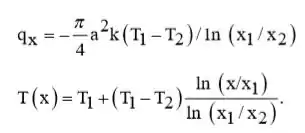
Passo 2
(b) A taxa de calor segue de
