Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 43
Medidas mostram que a condução em regime estacionário através de uma parede plana, sem geração de calor, produz uma distribuição de temperaturas convexa, de modo que a temperatura no centro é ΔTe superior àquela que seria esperada para uma distribuição de temperaturas linear.
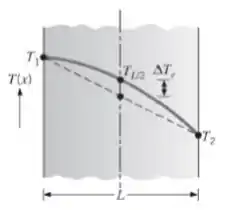
Supondo que a condutividade térmica apresente uma dependência linear com a temperatura, na qual a é uma constante, desenvolva uma relação para determinar a em termos de ΔTe, T1 e T2.
Passo 1
Beleza galerinha, vamos lá! Em qualquer localização na parede, a lei de Fourier tem a forma:
Como é uma constante, podemos separar Eq. (1), identificar limites de integração apropriados, e integrar para obter
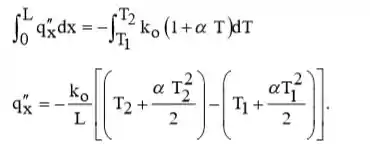
Passo 2
Poderíamos realizar a mesma integração, mas com os limites superiores em x = L/2, para obter
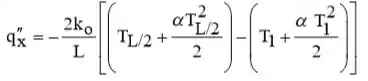
Onde,
Ajuste Eq. (3) igual a Eq. (4), substituição de Eq. (5) por TL/2, e resolvendo,
