Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 31
31 - Um furo de diâmetro é perfurado através do centro de um bloco sólido de seção transversal quadrada com de lado. O furo atravessa o comprimento do bloco, que é de . O bloco tem condutividade térmica k = 150 W/(m · K). As quatro superfícies externas estão expostas ao ar ambiente, com e , enquanto óleo quente escoa através do furo podendo ser caracterizado por e . Determine a taxa de transferência de calor e as temperaturas superficiais correspondentes.
Passo 1
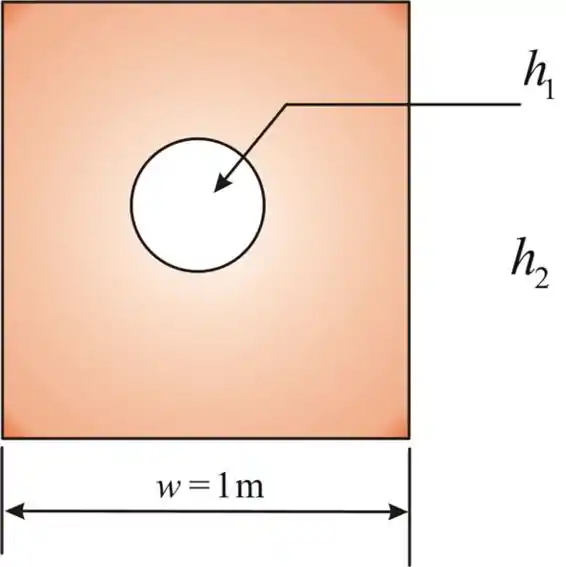
O diagrama representa que o furo é perfurado através do centro de um bloco sólido de seção transversal quadrada. A superfície externa é exposta ao ar ambiente e o óleo está fluindo através do orifício.
Passo 2
A taxa total de transferência de calor pode ser calculada como,
As resistências térmicas individuais podem ser calculadas como:
Resistência de condução,
Na tabela "Fatores de forma de condução" para o caso "cilindro circular de comprimento L centrado em um sólido quadrado de igual comprimento", o fator de forma é:
Passo 3
Então a resistência de condução é,
Passo 4
A resistência à convecção do óleo para a superfície do tubo é,
A resistência da convecção da superfície externa do bloco ao ar ambiente é,
Passo 5
A transferência de calor pode ser calculada a partir da equação.
Portanto, a transferência total de calor do bloco quadrado é .
Passo 6
A temperatura da superfície do furo pode ser calculada como,
Portanto, a temperatura da superfície do furo perfurado na seção transversal quadrada do bloco é .
Passo 7
A temperatura da superfície do bloco quadrado é,
Portanto, a temperatura da superfície da seção transversal quadrada do bloco é .