Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 18

A parede composta de um forno possui três materiais, dois dos quais com condutividade térmica, kA = 20 W/(m · K) e kC = 50 W/(m · K), e espessura LA = 0,30 m e LC = 0,15 m conhecidas. O terceiro material, B, que se encontra entre os materiais A e C, possui espessura LB = 0,15 m conhecida, mas a sua condutividade térmica kB é desconhecida.

Sob condições de operação em regime estacionário, medidas revelam uma temperatura na superfície externa do forno de Ts,e = 20°C, uma temperatura na superfície interna de Ts,i = 600°C e uma temperatura do ar no interior do forno de T∞ = 800°C. O coeficiente convectivo interno h é conhecido, sendo igual a 25 W/(m2 · K). Qual é o valor de kB?

Passo 1

Vamos analisar a questão juntos pra entendermos o que você deve fazer para revolvê-la.

Temos uma parede composta, onde calor está sendo transferido do interior do forno por convecção e ao longo da parede por condução:

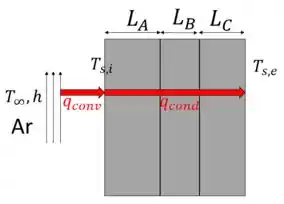
Fazendo um balanço de energia, podemos igualar os dois fluxos de transferência de calor e afirmar que todo o calor transferido do ar para a parede interna por convecção é igual ao calor transferido da parede interna para a externa por condução, de acordo com:

q c o n v =   q c o n d

A questão quer, então, que a gente encontre a condutividade térmica da parede B ( k B ). Para isso, vamos primeiro calcular o fluxo de transferência de calor por convecção. Depois, vamos igualar isso ao fluxo de calor por condução que pode ser encontrada a partir das resistências térmicas, e poderemos encontrar k B .

Antes de irmos pro Passo 2, quero que você guarde algumas propriedades que vamos utilizar:

L A = 0,3   m , L B = L C =   0,15   m   k A = 20 W m   ·   K ,   k C = 50 W m   ·   K   h = 25 W m 2 . K T ∞ =   800   ° C ,   T s , i = 600   ° C ,     T s , e = 20   ° C  

Passo 2

Em primeiro lugar, vamos calcular o fluxo convectivo a partir da equação:

q c o n v = h T ∞ - T s , i = 25 W m 2 . K 800   ° C - 600   ° C = 5000   W / m ²

Agora, vamos montar uma expressão para encontrar q c o n d a partir do seu circuito térmico:

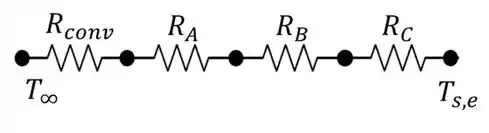
Podemos notar que temos uma resistência à transferência de calor por convecção e três por condução. Sendo assim, o fluxo de calor condutivo pode ser expresso como:

q c o n d =   T ∞ - T s , e R c o n v + R A + R B + R C

Sendo assim, podemos calcular as resistências:

R c o n v = 1 h = 1 25 W m ² . K = 0,04   m ² K / W

R A = L A k A = 0,3   m 20 W m . K = 0,015   m ² K / W

R B = L B k B = 0,15 k B

R C = L C k C = 0,15   m 50 W m . K = 0,003   m ² K / W

Além disso, lembrando que q c o n d =   q c o n v , temos que:

5000   =   800   - 20   0,04 + 0,015 + 0,15 k B + 0,003 → k B = 1,53   m ² W / K

Resposta

Como demonstrado no Passo 2, k B = 1,53   m ² W / K .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um dormitório em uma grande universidade, construído há 50 anos, tem as paredes externas construídas com um forro, que tem k = 0,1W / ( m · K ) e espessura L = 30m m . Para reduzir a perda térmica no
Uma parede composta separa gases de combustão a 2400 ° C de um líquido refrigerante a 100 ° C , com coeficientes de transferência de calor no lado do gás e no do líquido iguais a 25 e 1000W / ( m 2 ·
Considere uma parede plana composta constituída por dois materiais com condutividades térmicas k A = 0,09W / ( m · K ) e k B = 0,03W / ( m · K ) e espessuras L A = 8m m e L B = 16m m . A resistência d
Considere um transistor de potência encapsulado em uma caixa de alumínio que é fixado em sua base a uma placa quadrada de alumínio de condutividade térmica k = 240W / m ⋅ K , espessura L = 8m m e larg
Um longo fio de Constantan de 1m m de diâmetro é soldado a topo à superfície de um grande bloco de cobre, formando uma junção de termopar. O fio se comporta como uma aleta, permitindo que o calor flua