Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 5.Exercício - Ex. 17
O jato de água de área incie com velocidade na pá solidária ao carro, que se move sem atrito num plano horizontal. O carro, ao se mover, por ação do jato, reboca um bloco de peso sobre um plano inclinado. Se entre a base do bloco, de área , e o plano inclinado existe uma camada lubrificante de óleo de espessura , pergunta-se: qual deve ser a velocidade do jato em m/s para que o bloco se movimente no plano inclinado com velocidade constante ?
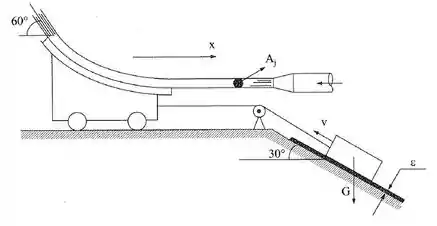
Passo 1
Vamos começar o exercício calculando a tensão no fio, que será a soma da força de cisalhamento na camada de óleo mais a componente do peso na direção do plano inclinado, então, assim, podemos escrever:
A força de cisalhamento é dada por:
Então, substituindo essa relação na equação anterior:
Substituindo os valores conhecidos, temos:
Passo 2
Agora vamos aplicar a equação da força exercida pelo fluido em um anteparo para a pá do problema, sendo 1 a entrada e 2 a saída do jato, a equação então se torna:
Vamos aplicar a equação na direção :
Como a vazão é constante e o diâmetro do jato também, então temos , e podemos escrever a vazão mássica como:
Substituindo essa expressão na equação para a força, temos:
Passo 3
Para que o carrinho se mova com velocidade constante, ou seja, sem aceleração, então devemos ter:
Substituindo os valores conhecidos:
Agora, a vazão do jato será a velocidade encontrada mais a velocidade do carrinho , então, temos: