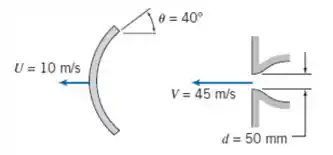
O prato circular, cuja seção transversal é mostrada, tem um diâmetro externo de . Um jato de água o atinge concentricamente e em seguida escoa para fora ao longo da superfície do prato. A velocidade do jato é e o prato move-se para a esquerda a uma velocidade de . Determine a espessura da lâmina de água em um raio de a partir do eixo do jato. Que força horizontal sobre o prato é requerida para manter o seu movimento?

Letra b)

Considerações Iniciais:

1. Escoamento em estado estacionário;
2. Escoamento incompressível;
3. Escoamento com velocidade constante ();
4. Escoamento Uniforme.

Pelas considerações feitas, utilizaremos a seguinte equação da quantidade de movimento:

Como estamos analisando um sistema , temos:

Não há forças de campo atuando no sistema, então :

Não temos a variação das propriedades com o tempo, então:

Assim:

Sendo que:

Então:

Desse modo, a força resultante se dá:

Para o fluxo de entrada, possuem uma inclinação de 180°, então .

Aqui, indica a velocidade relativa do fluxo de entrada, já , a velocidade relativa do fluxo de saída para as mesmas condições.

Onde:

;

.

Então:

Sendo:

;

.

;

;

.

Temos: