Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 149
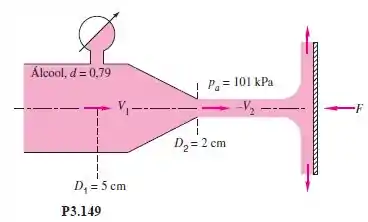
Um jato de álcool atinge a placa vertical da Figura . Uma força é necessária para manter a placa estacionária. Considerando que não há perdas no bocal, calcule (a) o fluxo de massa de álcool e (b) a pressão absoluta na seção .
Passo 1
E aí, tudo bem? Bora matar essa questão comigo!
Vamos fazer uma análise do momento linear placa linear (semelhante ao problema ), teremos a seguinte equação:
Agora resolvendo para , temos:
Assim:
Agora vamos encontrar de acordo com a conservação de massa:
Agora seguindo a equação de Bernoulli, temos:
Isso é tudo pessoal, conseguimos mais uma! \o/
Resposta
Exercícios de Livros Relacionados
4.107 Uma placa divisora de jato, de borda viva, inserida parcialmente em uma corrente plana de água, produz o padrão de escoamento mostrado. Analise a situação de modo a avaliar θ como uma função de
Uma fresta estreita entre duas placas circulares está inicialmente preenchida com líquido incompressível. Em t = 0 , a placa superior, inicialmente distate h 0 da placa inferior, começa a mover-se par
A água de um jato de diâmetro D é usada para suportar o objeto cônico mostrado. Deduza uma expressão para a massa combinada do cone e da água, M , que pode ser suportada pelo jato, em termos de parâme
No antigo Egito, vasos circulares cheios de água eram por vezes utilizados como relógios primitivos. Os vasos tinham um formato tal que, à medida que a água drenava pelo fundo, o nível da superfície d
Um fluido incompressível de viscosidade desprezível é bombeado com uma vazão volumétrica total Q por uma superfície porosa para o interior de uma pequena fresta entre placas paralelas estreitamente es