Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 62
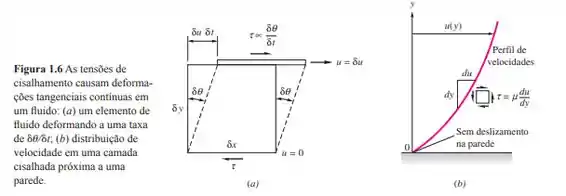
Mostre que o escoamento de Couette linear entre placas na Figura 1.6 tem uma função corrente, mas não tem potencial de velocidade. Qual é a razão disso?
Passo 1
Bora pra mais uma!
Devido a condição de não deslizamento, temos que a velocidade na parede será V=0. Podemos relacionar então o perfil de velocidades no eixo x com a altura em função de y, da forma que:
Daí, temos da continuidade:
Como a equação é satisfeita, isso nos traduz que a função corrente existe. Portanto:
Integrando em relação a y, temos:
Agora, integrando em relação a x:
Comparando as duas equações obtemos a função corrente:
Passo 2
Agora, da irrotacionalidade, temos:
Verifiquemos então se esta equação é igual a zero:
A equação acima nos traduz que o escoamento é rotacional, portanto, não há uma função potencial de velocidade.
Resposta
A função corrente conforme deduzida acima é
Onde C é uma constante.
E, pelo fato do escoamento ser rotacional, não há uma função potencial de velocidade.