Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 76
Um jato de ar, horizontal e assimétrico, com 10 mm, de diâmetro, atinge um disco vertical de 190 mm de diâmetro. A velocidade do jato é 69 m/s na saída do bocal. Um manômetro é conectado ao centro do disco. Calcule (a) a deflexão, se o líquido do manômetro tem SG = 1,75, (b) a força exercida pelo jato sobre o disco, e c) a força sobre o disco, se for considerado que a pressão de estagnação age sobre toda a superfície frontal do disco. Esboce a configuração de linhas de corrente e a distribuição de pressão sobre a face do disco.
Passo 1
Vamos começar ilustrando o problema em questão:
Agora vamos aplicar Bernoulli entre a saída do jato (ponto 1) e o ponto de estagnação (2), então, temos:
Nesse caso, como a saída do jato (ponto 1) está exposta ao ambiente, então , sabemos também que no ponto de estagnação . E como o enunciado não mencionou nada, podemos desprezar a diferença entre as cotas e , então a equação se torna:
Agora podemos aplicar o equilíbrio manométrico para o manômetro da figura, então temos:
Então, igualando as duas expressões para , temos:
E, substituindo os valores conhecidos, temos:
Passo 2
Agora para resolver a letra b), vamos aplicar a equação 4.18a de equilíbrio de momento para o sistema ilustrado no passo 1, então temos:
No nosso caso, estamos com um regime permanente, então podemos desprezar a primeira integral com a derivada no tempo, vamos desprezar também a ação da força de campo na direção , de modo que . Então a equação se torna:
Nesse caso, sabemos que e que , pois não temos componente de velocidade saindo nessa direção, então, a equação se torna:
Substituindo os valores conhecidos, temos:
Essa é a força exercida pelo disco exercida sobre o jato, então a força exercida pelo jato sobre o disco tem a mesma intensidade e sentido oposto, então temos:
Passo 3
Agora para calcular a força sobre o disco, se for considerado que a pressão de estagnação age sobre toda a superfície frontal do disco, vamos voltar à equação da pressão de estagnação encontrada no passo 1:
Como estamos interessados em pressão manométrica, podemos fazer , nesse caso a força exercida sobre o disco seria:
Substituindo os valores conhecidos, temos:
Passo 4
Para encontrar a distribuição de pressão, vamos começar aplicando Bernoulli entre a extremidade do disco (1) e um ponto qualquer (2) a uma distância radial do centro do disco, então, temos:
Nesse caso, sabemos que a extremidade do disco está em contato com o ambiente, então temos e podemos desprezar a diferença de cotas e . Agora precisamos encontrar uma função para a velocidade num ponto qualquer, para isso vamos usar a equação da vazão, nesse caso, para um disco circular, a vazão se torna:
Da continuidade, sabemos que essa vazão tem que ser igual a vazão que chega saindo do jato, dada por:
Então, igualando as duas expressões para a vazão, temos:
Nesse caso, precisamos estimar uma altura , vamos adotar para facilitar os cálculos, então, a equação para a velocidade se torna:
A velocidade na extremidade é dada por:
Passo 5
Substituindo as expressões encontradas na equação de Bernoulli do passo 4, temos:
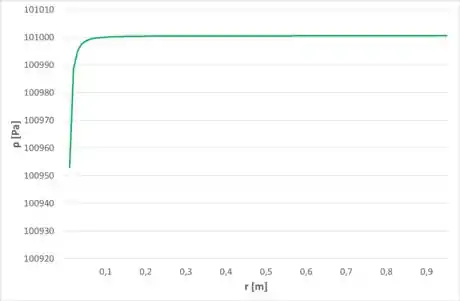
Substituindo os valores conhecidos, temos:
Plotando esse gráfico, temos:
