Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 74
Água escoa por uma torneira de cozinha de 1,25 cm de diâmetro com vazão de 0,1 L/s. O fundo da pia está 45 cm abaixo da saída da torneira. A área da seção transversal da corrente de água aumentará, diminuirá ou permanecerá constante entre a saída da torneira e o fundo da pia? Explique sucintamente. Obtenha uma expressão para a área da seção transversal da corrente como uma função da distância acima do fundo da pia. Se uma placa for mantida sob a torneira na posição horizontal, como variará a força requerida para segurar a placa com a altura da placa acima da pia? Explique sucintamente.
Passo 1
Tá legal, para começar vamos encontrar a velocidade com que a água sai da torneira usando a vazão fornecida, então temos:
Agora vamos aplicar Bernoulli entre a saída da torneira (ponto 1) e um ponto qualquer (2) a uma distância da torneira (distância que será medida a partir do fundo da pia, então, temos:
Nesse caso, como a saída da torneira (ponto 1) e o ponto 2 estão expostos ao ambiente, então e podemos cancelar os termos de pressão, dessa forma, a equação se torna:
Isolando dessa equação, temos:
Então, através da equação, podemos ver que a velocidade diminui conforme aumentamos (lembrando que cresce do fundo da pia em direção a torneira), então, podemos ver que a velocidade será máxima para , no fundo da pia. Isso quer dizer que conforme a água cai, a velocidade aumenta, isso ocorre porque a energia potencial que a água possuía lá em cima ao sair da torneira vai se transformando em energia cinética.
Passo 2
Agora vamos analisar a área da seção transversal da corrente de água, para isso, vamos utilizar o princípio da continuidade, onde temos que:
Substituindo os valores conhecidos, temos:
Dessa forma, podemos ver que a área da seção transversal da água diminui conforme a água cai da torneira, pois nesse caso, quando temos um valor de:
E quando
Ou seja, temos o valor máximo em , que está no ponto onde a água sai da torneira e o valor mínimo em , que está no fundo da pia.
Passo 3
Agora se tivermos uma placa abaixo da torneira, temos então a situação a seguir:
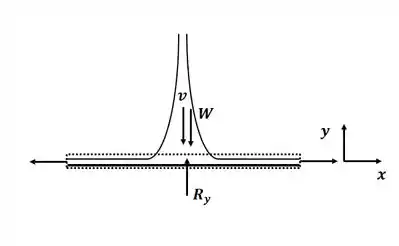
Então, para resolver esse item, vamos aplicar a equação de equilíbrio de momento 4.18b, e a equação tem a forma:
No nosso caso, estamos com um regime permanente, então podemos desprezar a primeira integral com a derivada no tempo, vamos desprezar também a ação da força de campo na direção , de modo que . Então a equação se torna:
E, nesse caso, sabemos que encontrado no passo 1, e que , pois não é na direção , então a equação se torna:
Como temos continuidade entre os pontos 1 e 2, podemos fazer:
Substituindo a expressão na equação anterior, temos:
Então, substituindo os valores conhecidos, temos:
Dessa forma, aumenta conforme a velocidade aumenta, ou seja, quanto mais perto do fundo da pia , maior é a força necessária para manter a placa em equilíbrio.