Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 9.Problemas - Ex. 37
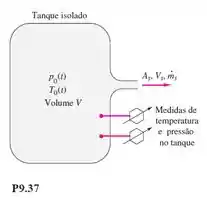
Faça uma análise exata de volume de controle do processo de esvaziamento na Figura P9.37, admitindo um tanque isolado com energias cinética e potencial desprezível dentro dele. Admita escoamento crítico na saída e mostre que tanto como decrescem durante o esvaziamento. Estabeleça equações diferenciais de primeira ordem para , simplifique e resolva o quanto puder.
Passo 1
Lets go, lets go!
Bora lá, temos que fazer as equações de massa e energia, comecemos pela massa, teremos que:
em que,
Já a equação de energia, desprezando energia cinética e potencial, teremos:
Passo 2
Podemos rearranjar essas duas equações e combinar elas, teremos uma equação diferencial para :
em que,
Por separação de variáveis, teremos:
Integrando,
Passo 3
Como já temos , agora só precisamos voltar no balanço de massa para encontrar nossa equação para , basta usar a hipótese de escoamento isentrópico, assim:
em que,
Resposta
Ei, a resposta está no passo a passo :)