Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 119
Retome a grade de turbina do Problema P3.78 e deduza uma fórmula para a potência P desenvolvida, usando o teorema da quantidade de movimento angular da Equação (3.55).
Passo 1
Simbora!!
Pela equação 3.55 e utilizando também o exemplo 3.14, pois já foi desenvolvido a análise de momento, teremos a seguinte expressão:
Retomando o Problema P3.78, lembremos do nosso esqueminha lindo, olha só:
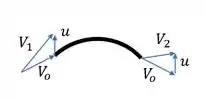
Aqui com .
Com ele, utilizando da trigonometria, encontraremos que:
em que, . As velocidades normais são iguais pela conservação de massa entre as lâminas!
Passo 2
Sabendo que, , teremos:
Resposta
Exercícios de Livros Relacionados
Um veículo-foguete, pesando 44.500N e viajando a 960k m / h , deve ser freado pelo abaixamento de uma concha para dentro de um reservatório de água. A concha tem 150m m de largura. Determine o tempo n
Uma corrente de água, na condição-padrão, sai de um bocal de 50 mm de diâmetro e atinge uma pá curva, conforme mostrado. Um tubo de estagnação conectado a um manômetro de em tubo U com água e instalad
Um bocal plano descarrega verticalmente para baixo 1200 L/s por unidade de largura na atmosfera. O bocal é alimentado com um fluxo permanente de água. Uma placa plana estacionária, inclinada, colocada
Um medidor Venturi, instalado em uma tubulação de água, consiste em uma seção convergente, uma garganta de área constante e uma seção divergente. O diâmetro do tubo é D = 100m m e o diâmetro da gargan
Dois grandes tanques contendo água têm pequenos orifícios de contornos lisos e arredondados e de áreas iguais. Um jato de líquido sai do tanque da esquerda. Considere que o fluxo seja uniforme e não a