Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 110
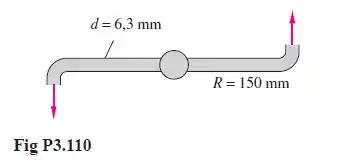
O irrigador de gramados horizontal da Figura P3.110 tem uma vazão d’água de 15,2 L/min, introduzida verticalmente pelo centro. Calcule (a) o torque resistente necessário para manter os braços sem rotação e (b) a rotação em rpm se não houver torque resistente.
Passo 1
Bora resolver essa juntos!
Tendo antes de mais nada que fazer uma conversãozinha, veja:
Temos que:
Do exemplo temos uma expressão para encontrar o torque necessário para manter o braço parado, pedido em (a), assim:
Braço parado quer dizer sem movimento angular, sem rotação, assim, , substituindo e isolando :
Passo 2
Se não houver torque, , teremos que a rotação do braço será dada por:
Resposta
- 0,3074 N.m
- 3240 rpm
Exercícios de Livros Relacionados
Um jato de ar horizontal com 13 mm de diâmetro, e axialmente simétrico, atinge um disco estacionário vertical com 203 mm de diâmetro. A velocidade do jato é de 69 m/s na saída do bocal. Um manômetro e
Um jato uniforme de água sai de um bocal de 15 mm de diâmetro e escoa diretamente para baixo. A velocidade do jato no plano de saída do bocal é 2,5 m/s. O jato atinge um disco horizontal e escoa radia
Você abre a torneira da cozinha muito lentamento, de modo que um filete de água escoa para a pia. Você nota que o escoamento é laminar e que isso se reforça para os primeiros 50 mm de descida. Para me
Um disco de 2 kg é restringido horizontalmente, mas está livre para mover na direção vertical. O disco é atingido por baixo por um jato vertical de água. Na saída do bocal, a velocidade e o diâmetro d
Estudantes estão brincando com uma mangueira de água. Quando eles a apontam para cima, o jato de água atinge apenas uma das janelas do escritório do Professor Pritchard, a 10 m de altura. Se o diâmetr