Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 118
Reverta o escoamento na Figura P3.116, de modo que o sistema passe a operar como uma turbina de fluxo radial. Considerando que o escoamento na seção de saída 1 não tem velocidade tangencial, deduza uma expressão para a potência P extraída pela turbina.
Passo 1
Bora lá bora lá!
Vamo lá, essa questão vai ser parecida com a P3.116. Teremos o torque sendo dado por:
Exatamente como na questão anterior, porém, teremos um diagrama de velocidade invertido, olha só:
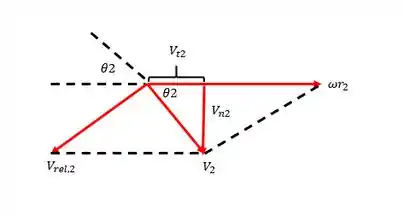
Assim, por trigonometria, a velocidade tangencial 2, será:
em que,
Passo 2
Sabendo que, , teremos:
Resposta
Exercícios de Livros Relacionados
Um bloco retangular de massa m , com faces verticais, rola sem resistência ao longo de um plano horizontal liso, conforme mostrado. O bloco viaja, inicialmente, à velocidade u 0 . Em t = 0 , ele é ati
Um jato vertical de água atinge um disco horizontal conforme mostrado. O peso do disco é igual a 30k g . No instante em que o disco encontra-se a 3m acima da saída do bocal, o seu movimento é para cim
Considere o enunciado e o diagrama do Problema 4.155. Considere que em t = 0 , quando o bloco de mass m = 5k g está em x = 0 , ele seja posto em movimento para a direita com velocidade u = 10m / s . O
Um veículo-foguete, com velocidade inicial de 300m / s , deve ser desacelerado pelo abaixamento de uma concha para dentro de um reservatório de água. A concha tem 0,3m de largura e deflete a água de 1
Partindo do repouso, o carrinho mostrado é propelido por uma catapulta hidráulica (jato de líquido). O jato atinge a superfície curva e é defletido de 180 ° , saindo na horizontal. As resistências de