Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 139

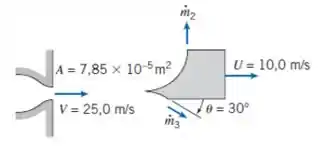
Um jato plano de água atinge uma pá divisora, repartindo-se em duas correntes planas, conforme mostrado. Determine a razão entre as vazões mássicas, m 2 m 3 ˙ ˙ , necessária para produzir uma força resultante vertical igual a zero sobre a pá divisora. Se há uma força resistiva de 16 N aplicada na pá divisora, determine a velocidade de regime permanente u da pá.

Passo 1

Considerações Iniciais:

  1. Escoamento em estado estacionário;
  2. Escoamento incompressível;
  3. Escoamento com velocidade constante;
  4. Escoamento uniforme;

Passo 2

Pelas considerações feitas no passo 1, utilizaremos a seguinte equação da quantidade de movimento:

F = ∂ ∂ t ∫ V C V ρ   d ∀ + ∫ S C V ( ρ V ) d A = 0

Como estamos analisando um sistema y , temos:

F y = ∂ ∂ t ∫ V C v ρ   d ∀ + ∫ S C v ( ρ V ) d A

Não temos a variação das propriedades com o tempo, então:

∂ ∂ t = 0

Assim:

F y = ∫ S C v ( ρ V ) d A

F y = ∑ S C v ⋅ m ˙

Passo 3

F y = ∑ S C v ⋅ m ˙

Para o fluxo de entrada, V   e   A possuem uma inclinação de 180°, então m 1 ˙ = ( - m ˙ 1 ) .

F y = v 1 ⋅ - m 1 ˙ + v 2 ⋅ m 2 ˙ + v 3 ⋅ m 3 ˙ ˙

Sendo:

v 1 = 0 ;

v 2 = ( v - u ) ;

v 3 = - v - u ⋅ s e n   θ .

Então:

F y = 0 ⋅ - m 1 ˙ + v - u ⋅ m 2 ˙ + - v - u ⋅ s e n   θ ⋅ m 3 ˙ ˙

Sendo que não há força em y , então, F y = 0 .

0 = v - u ⋅ m 2 ˙ + - v - u ⋅ s e n   θ ⋅ m 3 ˙ ˙

v - u ⋅ m 2 ˙ = v - u ⋅ s e n   θ ⋅ m 3 ˙

m 2 m 3 ˙ ˙ = s e n   θ

Sendo θ = 30 ° :

m 2 m 3 ˙ ˙ = s e n   30 ° = 1 2

Passo 4

Para determinarmos a velocidade de regime permanente u da pá, temos que primeiramente encontrar a vazão mássica de água que atinge a pá do separador:

m 1 ˙ = v - u ρ A = 25 - u ⋅ 1000 ⋅ 7,85 x 10 - 5 = 0,0785 ⋅ ( 25 - u )

Agora, devemos analisar a seguinte relação:

m 1 ˙ = m 2 + m 3 ˙ ˙

Como m 2 m 3 ˙ ˙ = 1 2

Podemos concluir que:

m 1 m 3 ˙ ˙ = 1 2 + 1 = 3 2

m 3 = 2 m 1 ˙ 3 ˙ = 2 3 ⋅ [ 0,0785 ⋅ 25 - u ]

Passo 5

Para a equação de quantidade de movimento horizontal, temos:

F x = u 1 ⋅ - m 1 ˙ + u 2 ⋅ m 2 ˙ + u 3 ⋅ m 3 ˙ ˙

v 1 = ( v - u ) ;

v 2 = 0 ;

v 3 = v - u ⋅ c o s   θ .

Então:

F x = ( v - u ) ⋅ - m 1 ˙ + 0 ⋅ m 2 ˙ + v - u ⋅ c o s   θ ⋅ m 3 ˙ ˙

Sendo:

F x = - 16   N ;

v = 25   m / s ;

m 1 ˙ = 0,0785 ⋅ ( 25 - u ) ;

m 3 = 2 m 1 ˙ 3 ˙ = 2 3 ⋅ [ 0,0785 ⋅ 25 - u ] ;

θ = 30 ° .

Temos:

- 16 = ( 25 - u ) ⋅ - 0,0785 ⋅ 25 - U + 25 - u ⋅ c o s   30 ° ⋅ 2 3 ⋅ [ 0,0785 ⋅ 25 - U ] ˙

u = 3,03   m / s

Resposta

m 2 m 3 ˙ ˙ = 1 2

u = 3,03   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considerando que na região de escoamento completamente desenvolvido de um tubo, a integral da quantidade de movimento axial é a mesma em todas as seções transversais, explique a razão para a queda de
Para as condições do Problema 4.34, avalie a razão entre o fluxo de quantidade de movimento na direção x na saída do canal e aquele na entrada.
Para as condições do Problema 4.35, avalie a razão entre o fluxo de quantidade de movimento na direção x na saída do canal e aquele na entrada.
Jatos de água estão sendo usados cada vez com maior frequência para operações de cortes de metais. Se uma bomba gera uma vazão de 63 x 10 - 6m 3 / s através de um orifício de diâmetro 0,254m m , qual
Avalie a taxa líquida de fluxo de quantidade de movimento para fora da superfície de controle do Problema 4.24.